[expand title=”How can I simplify it?”]
In previous lessons you have worked with expressions, combinations of numbers, variables, and operation symbols,that involve either adding integers or multiplying integers. Today you will examine expressions that involve both operations. By the end of this lesson, you will be expected to be able to answer these target questions:
How can expressions with the same numbers and operations
have different meanings?
Does the order in which we do each operation matter?
3-1. Katrina wrote the following set of instructions for Cecil: 4 · 2.5 + 1.
1. If Cecil the acrobat follows Katrina’s instructions, how far will he go? Draw a diagram of Cecil’s movements and show how far he will move.
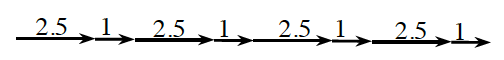
2. Katrina drew the diagram at right. How was she thinking about Cecil’s moves? Write an expression to represent Katrina’s diagram.
3. Explain why Katrina’s diagram in part (b) will not give her the correct length for 4 · 2.5 + 1.
4. Cecil changed Katrina’s set of instructions so that the length of 1 foot came first, as shown in the diagram at right. Write an expression to represent this new diagram. How far does Cecil move here? Does this give the same length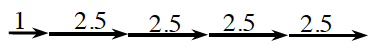 
as 4 · 2.5 + 1?
3-2. Cecil’s trainers proposed each of the following movements. Which one requires the longest rope? Draw diagrams to justify your answer.
- 8 + 2(6.48) feet
- 2 + 8(6.48) feet
- (8 + 2)6.48 feet
3-3. The expression 5 + 3 · 4 + 2 can be used to represent the group of + t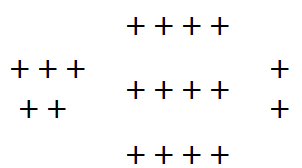
iles shown at right.
- Work with your team to explain how each part of the expression connects with the groups of + tiles. How many tiles are there?
- Each group of + tiles is represented by a different part of the expression, also called a numerical term. Numerical terms are single numbers or products of numbers. It is often useful to circle terms in an expression to keep track of separate calculations. For example, each term circled in the expression below represents a separate part of the collection of + tiles above.
Circle the terms in the expression shown below. Then explain what each term could describe about collections of + or – tiles.
4 · 5 + 1 + 3(–2) + 6
3-4. Circle the terms and simplify each expression shown below. Simplify means to write an expression in its simplest form. In the case of numerical expressions, the simplest form is a single number.
- 7.08 + 2.51 + (−3.84)
- 7.8 + 2.1(−3)
- 5(−
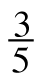)+ 2 · 1.5 - 4.35 · 2 + 5 +3
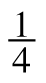(−1) + (−10)
3-5. GROUPING CHALLENGE
Work with your team to add parentheses to 1 + 3 · 2 + 8 + (−4) so that the resulting expression has the smallest possible value. Then find a different way to add parentheses to the same expression so that it has the largest possible value. For each expression, draw a diagram of how Cecil would move.
Assignment: 3.1.1 Homework
[/expand]
[expand title=”What if they are complicated?”]
In today’s lesson, you will continue to simplify expressions using the correct Order of Operations. You will also learn how to identify terms in expressions that are more complicated.
3-14. Consider the expression 3(5 + 2 · 4) + 2(−3).
- Work with your team to draw a diagram representing this expression. Your diagram could show Cecil’s movements, for example, or it could show + and – tiles that could be represented by this expression.
- Simplify the expression.
- Discuss with your team how you might circle terms in this expression. Be ready to explain your ideas to the class.
3-16. AIM FOR 16
- In this game, you and the other players will create expressions that contain the same four numbers. Then you will compare the numbers that your expressions represent to see whose number is closest to 16.
- Your teacher will roll four number cubes or use 3-16 Number Cubes (CPM) to virtually roll four number cubes to determine the four numbers you can use in your expression. You may use each number as either a positive or negative integer, and each number must appear exactly once in your expression. For example, if a number cube lands on 5, you can use either 5 or −5 in your expression. Try to make an expression that represents a number that is as close to 16 as possible.
- Your score is how far your expression’s value is from 16. For example, for an expression that represents 20, the score would be 4, and for an expression that represents 13, the score would be 3. Compare your expression with your opponent’s. Whoever has the lowest score wins that round. As you continue playing more rounds, keep track of your total score and try to keep it as low as you can.
3-17.Additional Challenge: Simplify each of the expressions below. For each one, be sure to show your work or explain your reasoning.
- (4 + 2(−5) + 3(2 + (−3)) + 2) 6 + (−2)
- (9 + 3(−2 + 4)) + (6 + 2(5 + (−7)) + 1)
Assignment: 3.1.2 Homework
[/expand]
[expand title=”How can I subtract?”]
In Chapter 2, you worked with adding and multiplying integers (positive and negative whole numbers and zero). In this lesson, you will use + and – tiles to learn about subtraction of integers. Keep the following questions in mind as you work with your team today. At the end of the lesson, you will discuss your conclusions about them.
How can we remove negative tiles when the collection has only positive tiles?
How can we think about subtraction when there are not enough to “take away”?
When does subtracting make the result larger?
3-24. Examine the assortment of positive and negative tiles at right. What integer does this assortment represent? Explore using the 3-24 Student eTool (CPM).
- What happens if three + tiles are removed? How can you use numbers and symbols to represent this action and the resulting value?
- What happens if three – tiles are removed from the original set of tiles? Again, how can you represent this action and the result using numbers and symbols?
3-25. It is often useful to represent operations and expressions in multiple ways. These ways include:
- A diagram (for example, using + and – tiles or with a number line)
- A numerical expression
- A situation described in words
- The total value
In each part labeled (a) through (c) below, one representation is given. Work with your team to create each of the other representations. Explore using the 3-25 Student eTool (CPM).
- −8 −(−3)
- It is cold! The first time I looked at the thermometer today, it said it was 0 degrees Fahrenheit. Then it dropped 5 degrees! How cold is it now?
3-26. Note: Before you start this problem, you may want to review the Math Notes box in Lesson 2.2.4. It will remind you of how to use + and – tiles to represent integer addition.
For each of the expressions below:
- Build an assortment of tiles that represents the first integer.
- Explain how to subtract using words.
- Find a way to draw the process on your paper.
- Record the expression and result as a number sentence.
- 7 − 5
- 0 − 4
- −6 − 2
- 3 − (−4)
- −8 − (−5)
- −1 − (−9)
3-27. Subtraction can also be represented on the number line model.
- Sketch the number line above on your paper.
- How can you represent 2 − 7 using the number line? Discuss your ideas with your team and use the number line to represent your answer.
- How can you represent 1 − (−2) using the number line? Again, discuss your ideas with your team and use the number line to represent your answer.
3-28. The Deep Submergence Vehicle, Alvin, can dive to a maximum depth of 14,764 ft. If sea level is 0, then this depth can be written as –14,764 ft. The deepest point in the Pacific Ocean, as well as the world, is a location called Challenger Deep in the Mariana Trench. It has a depth of –35,840 ft. Tory and Nina wanted to know the distance from the bottom of the trench to Alvin when the submarine was at its maximum dive depth.
Tory knew that they needed to subtract to find the difference between the two depths, so she did −35,840 − (−14,764), Nina, on the other hand, did −14,764 − (−35,840).
- Complete both computations. What do you notice about the solutions?
- If you want to find the distance between the two depths, what could you do with the computations to get a positive value? Write both expressions to show this.
- Use your work from part (b) to find the distance between Alvin at its deepest dive depth and the following points. For each calculation, write an equation and your solution.
- The Puerto Rico Trench in the Atlantic Ocean, –28,374 ft.
- The Eurasia Basin in the Arctic Ocean, –17,881 ft.
- The Java Trench in the Indian Ocean, –23,376 ft.
3-29. Absolute value can be thought of as the distance between a number and zero, but it can be thought of as the distance between two non-zero numbers, as well. Use your number line model from problem 3-27 to answer the following questions.
- Place points at 8.6 and 3.4 on your number line. What is the absolute value (distance) between 8.6 and 3.4? How can you tell?
- Use the number line to find the absolute value (distance) between –6.72 and 4.13.
3-30. Represent the distance between each pair of points below in two ways using the absolute value symbol. For example, the distance between 8 and 3 can be written = 5 as well as = 5.
- −2 and 1
- 2.38 and 7.49
- 9 and −6.55
3‑31. Zariah drew the diagram at right to show Cecil the acrobat’s movements on a tightrope.
Her expression is 8 + (−3) + 2. Discuss with your team how the numbers in her expression are related to the diagram.
Zariah decided to change the length of the acrobat’s sequence by removing the 2‑foot arrow. How does this change the length of the sequence? How can this action (removing the 2‑foot arrow) be represented in a number sentence?
What if Zariah removed the 3-foot-long arrow instead, leaving both of the other arrows in the diagram above? How does removing this movement change the overall length of the sequence? How can this action (removing the backwards 3‑foot arrow) be represented in her expression? How can it be represented by changing the diagram? Discuss this with your team or the class until the way the expression is written makes sense.
3-32. Additional Challenge: Add parentheses to make each subtraction equation true.
- 1 − 3 − 5 − 7 = 0
- 1 − 3 − 5 − 7 = −14
- 1 − 3 − 5 − 7 = −4
- 1 − 3 − 5 − 7 = 10
3-33. With your team, discuss the questions that appear at the beginning of this lesson. (They are reprinted below.) Be prepared to explain your ideas to the class.
- How can we remove negative tiles when
- the collection has only positive tiles?
- How can we think about subtraction when there are
- not enough to “take away”?
- When does subtracting make the result larger?
Assignment: 3.1.3 Homework
[/expand]
[expand title=”How can I subtract?”]
In Chapter 2, you worked with adding and multiplying integers (positive and negative whole numbers and zero). In this lesson, you will use + and – tiles to learn about subtraction of integers. Keep the following questions in mind as you work with your team today. At the end of the lesson, you will discuss your conclusions about them.
3-24. Examine the assortment of positive and negative tiles at right. What integer does this assortment represent? Explore using the 3-24 Student eTool (CPM).
- What happens if three + tiles are removed? How can you use numbers and symbols to represent this action and the resulting value?
- What happens if three – tiles are removed from the original set of tiles? Again, how can you represent this action and the result using numbers and symbols?
3-25. It is often useful to represent operations and expressions in multiple ways. These ways include:
- A diagram (for example, using + and – tiles or with a number line)
- A numerical expression
- A situation described in words
- The total value
In each part labeled (a) through (c) below, one representation is given. Work with your team to create each of the other representations. Explore using the 3-25 Student eTool (CPM).
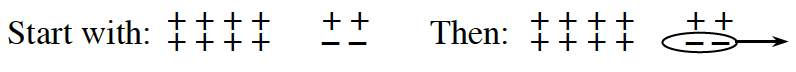
- −8 −(−3)
- It is cold! The first time I looked at the thermometer today, it said it was 0 degrees Fahrenheit. Then it dropped 5 degrees! How cold is it now?
3-26. Note: Before you start this problem, you may want to review the Math Notes box in Lesson 2.2.4. It will remind you of how to use + and – tiles to represent integer addition.
For each of the expressions below:
- Build an assortment of tiles that represents the first integer.
- Explain how to subtract using words.
- Find a way to draw the process on your paper.
- Record the expression and result as a number sentence.
- 7 − 5
- 0 − 4
- −6 − 2
- 3 − (−4)
- −8 − (−5)
- −1 − (−9)
3-27. Subtraction can also be represented on the number line model.
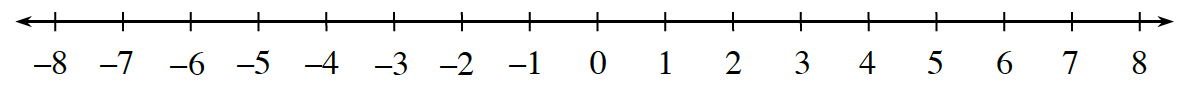
- Sketch the number line above on your paper.
- How can you represent 2 − 7 using the number line? Discuss your ideas with your team and use the number line to represent your answer.
- How can you represent 1 − (−2) using the number line? Again, discuss your ideas with your team and use the number line to represent your answer.
3-28. The Deep Submergence Vehicle, Alvin, can dive to a maximum depth of 14,764 ft. If sea level is 0, then this depth can be written as –14,764 ft. The deepest point in the Pacific Ocean, as well as the world, is a location called Challenger Deep in the Mariana Trench. It has a depth of –35,840 ft. Tory and Nina wanted to know the distance from the bottom of the trench to Alvin when the submarine was at its maximum dive depth.
Tory knew that they needed to subtract to find the difference between the two depths, so she did −35,840 − (−14,764), Nina, on the other hand, did −14,764 − (−35,840).
- Complete both computations. What do you notice about the solutions?
- If you want to find the distance between the two depths, what could you do with the computations to get a positive value? Write both expressions to show this.
- Use your work from part (b) to find the distance between Alvin at its deepest dive depth and the following points. For each calculation, write an equation and your solution.
- The Puerto Rico Trench in the Atlantic Ocean, –28,374 ft.
- The Eurasia Basin in the Arctic Ocean, –17,881 ft.
- The Java Trench in the Indian Ocean, –23,376 ft.
3-29. Absolute value can be thought of as the distance between a number and zero, but it can be thought of as the distance between two non-zero numbers, as well. Use your number line model from problem 3-27 to answer the following questions.
- Place points at 8.6 and 3.4 on your number line. What is the absolute value (distance) between 8.6 and 3.4? How can you tell?
- Use the number line to find the absolute value (distance) between –6.72 and 4.13.
3-30. Represent the distance between each pair of points below in two ways using the absolute value symbol. For example, the distance between 8 and 3 can be written
= 5 as well as 
= 5.
- −2
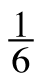and 1 - 2.38 and 7.49
- 9
and −6.55
3‑31. Zariah drew the diagram at right to show Cecil the acrobat’s movements on a tightrope.
- Her expression is 8 + (−3) + 2. Discuss with your team how the numbers in her expression are related to the diagram.
- Zariah decided to change the length of the acrobat’s sequence by removing the 2‑foot arrow. How does this change the length of the sequence? How can this action (removing the 2‑foot arrow) be represented in a number sentence?
- What if Zariah removed the 3-foot-long arrow instead, leaving both of the other arrows in the diagram above? How does removing this movement change the overall length of the sequence? How can this action (removing the backwards 3‑foot arrow) be represented in her expression? How can it be represented by changing the diagram? Discuss this with your team or the class until the way the expression is written makes sense.
3-32. Additional Challenge: Add parentheses to make each subtraction equation true.
- 1 − 3 − 5 − 7 = 0
- 1 − 3 − 5 − 7 = −14
- 1 − 3 − 5 − 7 = −4
- 1 − 3 − 5 − 7 = 10
3-33. With your team, discuss the questions that appear at the beginning of this lesson. (They are reprinted below.) Be prepared to explain your ideas to the class.
How can we remove negative tiles when
the collection has only positive tiles?
not enough to “take away”?
When does subtracting make the result larger?
Assignment: 3.1.3 Homework
[/expand]
[expand title=”What patterns can I find?”]
You have investigated relationships between addition and multiplication as well as subtraction and multiplication. You also know that multiplication and division are closely related. Are these the only relationships between operations? Today you will investigate this question as you look for relationships between the subtraction and addition.
3-39. Put ten – tiles on your table. With your team, find at least four different sequences of steps (adding or removing any number of + or – tiles in each step) to end up with tiles that represent –4. Represent each of these methods with an expression.
- Are any of your expressions or methods more efficient than others? Is it possible to combine movements or steps so that you can complete the task in only one step?
- How many different expressions can you create that accomplish this task in only one step? Be prepared to share your conclusions with the class.
3-40. Now start with five + tiles and find ways to end up with only two + tiles. Use your ideas from problem 3-39 above to find the two most efficient ways to do this with only one step. Describe how the two expressions accomplish the same task.
3-41. Rewrite the expression 7 − (−2) as an addition expression that gives the same result. Justify your addition expression using the integer tiles.
3-42. HOW CAN WE REWRITE IT?
Do you think that every subtraction problem can be rewritten as an addition problem that gives the same result?
Your Task: Work with your team to develop a convincing argument to answer this question. You may use examples from the list below or make up your own.
|
6 + (−2)
|
6 − 2
|
7.85 − (−5)
|
7.85 + 5
|
|
–
– |
–
+(–) |
−8 − (−12)
|
−8 + 12
|
|
0 − 5
|
0 + (−5)
|
0 − (−0.125)
|
0 + 0.125
|
3-43. When would rewriting subtraction problems into addition problems be useful? With your team, decide which of the following expressions you may want to rewrite and why. Be prepared to share your reasons with the class.
- −100.86 − (−3.86)
- 21 − (−7)
- −24 − 6
- –
–
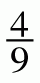- 0 − 1.12
- 0 − (−37)
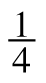3-44. Work with your team to represent the following problem in at least two ways. First, represent it as an expression containing only addition. Second, represent it as an expression containing addition and subtraction. Be prepared to explain to your class the ways that you see it.
While traveling in France, Juno was entertaining himself by riding in an elevator in a very tall building. He started at the ground floor (which in France is considered the 0th floor) and went up 26 floors. Then he rode down 7 floors. Next, he went up another 3 floors and then down again another 16 floors. What floor did Juno end up on?
3-45. LEARNING LOG
In your Learning Log, explain how subtraction and addition are related. Include several examples with diagrams to justify your response. Title this entry “Connecting Addition and Subtraction” and label it with today’s date.
Assignment:
[/expand]
[expand title=”How can I multiply integers?”]
In this lesson, you will work with your team to continue thinking about what happens when you remove + and – tiles from a collection of tiles representing a number. You will extend your thinking to find ways of making your calculations more efficient when the same number of tiles are removed multiple times. Consider these questions as you work today:
adding and multiplying integers in Chapter 2?
3-51. For each expression below, predict what you know about the result without actually calculating it. Can you tell if the result will be positive or negative? Can you tell if it will be larger or smaller than the number you started with? Be ready to explain your ideas.
- −1 − (−6.5)
- 2.2 − (−2.2)
- 12
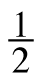− 22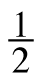 - −100 − (−98)
- −10 − (−2) − (−2) − (−2)
3-52. Now draw (or describe) a diagram for each of the expressions in problem 3‑51 and calculate the number that each of them represents.
3-53. Troy and Twana are working with the expression −10 −(−2) − (−2) − (−2) from part (e) of problem 3-51.
- Help them find a shorter way to write this expression.
- Imagine that their expression does not include the –10. How could they write the new expression? What number would this new expression represent? If you were to describe what this expression represents using + and – tiles, what would you say?
3-54. How could you evaluate the product −7(−11) ? Work with your team to make sense of −7(−11) . Prepare a brief presentation explaining why your result must be correct.
3-55. WHAT DOES IT MEAN?
Your Task: Work with your team to create a poster that shows what it means to multiply a negative number by another negative number or to multiply a negative number by a positive number. To demonstrate your ideas, include:
- Examples (from the list below or create your own).
- Pictures or diagrams.
- Any words necessary to explain your thinking.
- Numerical sentences to represent each of your examples.
| 4(−3) | −4(−3) | −4(3) |
| 2(−7) | −2(−7) | −2(7) |
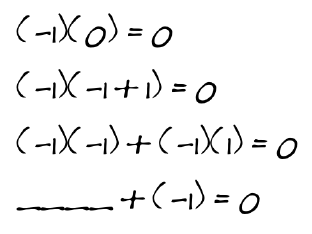
3-56. Marcy asked Dario, “Why is (−1)(−1) = 1?” Dario helped her by writing the steps at the right. Copy, complete, and give a reason for each of Dario’s steps to explain to Marcy why (−1)(−1) =1.
3-57. What does −18 ÷ 9 equal? How do you know? Explain why your answer makes sense. Then complete the division problems below.
- 45 ÷ (−3)
- −32 ÷ (−8)
- −54 ÷ 6
3-58. LEARNING LOG
In your Learning Log, describe what you understand about the product of two negative numbers and the product of a negative number and a positive number. Also describe how this is related to division with negatives. Give several examples. Title this entry “Multiplying and Dividing With Negative Numbers” and label it with today’s date.
Assignment:3.2.3 Homework
[/expand]
[expand title=”How does this work with decimals?”]
Just like “decade” is another name for ten years, a “decimal” number is a number that can be written as a fraction whose denominator is a power of ten (10, 100, 1000 etc.). Because our entire number system is based on ten, decimals are very important – and they are everywhere! Much of the math you see in science class uses decimals. Of course, you also use them whenever you work with money. Today you will practice working with decimals using what you know about fractions to make sense of the standard algorithm for multiplying decimals. As you work with your team, keep these questions in mind:
3-64. Howard went to the mall and saw a banner announcing, “ALL SPORTING GOODS: ONE TENTH OFF!” He saw a pair of roller-blade laces for $0.40 and wanted to find out how much he would save. With your team, follow the steps below to help Howard determine his savings.
Obtain a copy of the Lesson 3.2.4 Resource Page (“Hundredths Grids”) or use the Base 10 Blocks (CPM). It contains several copies of “hundredths grids,” which you will be using throughout this lesson. Hundredths grids are larger versions of unit tiles. Each side measures one unit, divided into ten equal parts.
- What is the perimeter of each hundredths grid? What is the area?
- What do each of the small squares in the grid represent? Write your answer in three forms (fraction, decimal, and percent).
- Why do you think these are called “hundredths grids?”
- Forty cents (the cost of Howard’s laces) can also be written as 0.40, or simply 0.4. On your resource page of hundredths grids, lightly shade and label 0.4 or
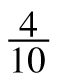vertically, as shown in the diagram at right.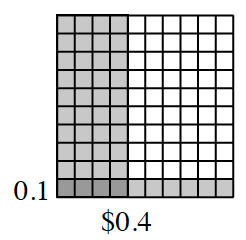
- Next, in the other direction, lightly shade and label
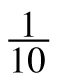of the grid as shown in the diagram at right. What is the fraction of the grid that is darkly shaded? What is the decimal equivalent of the part of the grid that is darkly shaded? - Write two equations that represent this process, one using fractions and one using decimals.
- How much money will Howard save with the laces on sale?
3-65. While in the sporting-goods store, Howard found some new running shoes advertised to weigh only 70% as much as his old running shoes. His old shoes weighed 0.8 kg. Use the problems below to determine how much these new shoes weigh.
- Use a hundredths grid to find 70% of 0.8 kg.
- Write a fraction equation for this problem. Label the answer with correct units.
- Write a decimal equation for this problem. Label the answer with correct units.
- Do the new shoes weigh more or less than the old shoes? How much more or less?
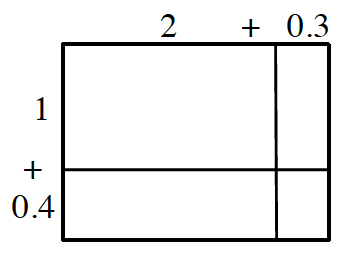
3-66. Another way to think about decimal multiplication is with a generic rectangle.
- What multiplication problem is represented by the generic rectangle shown at right? On your paper, copy this rectangle and write the multiplication problem it represents.
- Fill in the areas of each of the four sections. What math problem does each smaller section represent?
- Write the total area as both a sum and a product. Does your answer make sense?
- Use the standard paper-and-pencil method of multiplying 2.3 by 1.4. Do not use a calculator. Where do you see the numbers from this standard algorithm in the generic rectangle?
3-67. Judy is working on part (d) of problem 3-66 and is trying to make sense of the standard algorithm for decimal multiplication. Her work so far is shown at right.
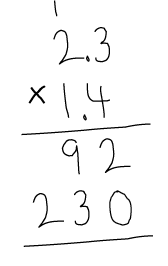
“Wait a minute,” Judy said, “I multiplied 2.3 by 0.4 and then by 1. How in the world could those products be 92 and 230? That just doesn’t make sense.”
- The decimal points are usually left out of a multiplication problem until the last step. You can see that Judy left them out in her work above. If the decimal points were to be put in, where would they go in each line of her work? That is, is 2.3 times 0.4 equal to 92, 9.2, or 0.92? And then in the next line, is 2.3 times 1.0 equal to 230, 23.0, or 2.30?
- Copy Judy’s work on your paper and place the decimal points in the correct locations. Then complete the work. What is 2.3 times 1.4?
3-68. When multiplying decimals, how do you know where to place the decimal point? Think about this as you do parts (a) through (d) below.
- Write two equations for multiplying 0.3 by 0.16. One equation should express the factors and product using decimals, and one using fractions.
- In part (a), you multiplied tenths by hundredths to get thousandths. Do you always get thousandths if you multiply tenths by hundredths? Why or why not? What do you get if you multiply tenths by tenths? Hundredths by hundredths? Use several examples to justify your answers.
- When a multiplication problem is written using decimals, there is a relationship between the number of decimal places in the parts (or factors) of the problem and the number of decimal places in the answer (or product). Describe this relationship.
- Describe a shortcut for locating the decimal point in the answer to a problem involving decimal multiplication.
3-69. For each of the following problems, use a hundredths grid if needed. Write both a fraction and a decimal equation with your answer.
- (0.3)(0.6)
- (0.5)(−0.4)
- −0.2 · −0.7
3-70. Jerry’s teacher gave him the problem (−2.4)(5.3). He decided to use a generic rectangle to find the answer. He used the generic rectangle below and found that (−2.4)(5.3) = 
−8.48.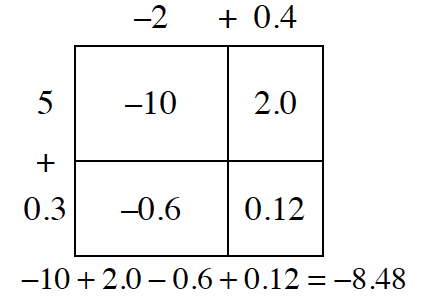
- Jerry’s teammate Ron knows that (2.4)(5.3) = 12.72, so he thinks that the answer to (−2.4)(5.3) is −12.72.
- Who is correct, and what was the mistake that was made by the incorrect student?
3-71. Draw generic-rectangle diagrams and write equations to find the following products.
- (−6.5)(−4.7)
- (−3.8)(4.4)
3-72. Howard, in his new lightweight running shoes, was able to walk at the rate of 0.83 meters per second. His coach timed his walking at this steady pace for 12.2 seconds. How far did he walk during that time? Use paper and a pencil to show your work, and then check your answer with a calculator.
Assignment:3.2.4 Homework
[/expand]
[expand title=”What can I do with integers?”]
In this lesson, you will have an opportunity to practice adding, subtracting, multiplying, and dividing integers as you play a game against a partner. As you play, consider these questions:
Which operation with these integers will move us farthest?
Obtain a Lesson 3.2.5 Resource Page from your teacher or use the Tug-O-War eGame (CPM) and play Tug-o-War against your partner. Keep track of any strategies that you use or discover as you are playing. Play until your teacher calls time. The rules are printed below.
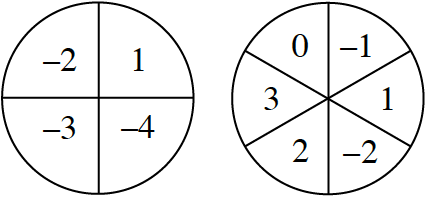
How to Play
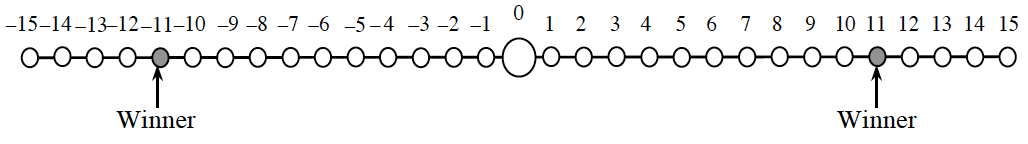
3-79. With your team and then as a class, discuss any strategies that you used or discovered as you played the Tug-o-War game. Use the focus questions at the beginning of this lesson to guide your discussion.
3-80. Cynthia, Devin, Gavin, and Mark are playing the Tug-O-War game.
- Cynthia begins her turn with her marker at 15. She spins a 1 and a –3. She thinks that she might be able to get to the winner space at 11 with this spin. Is she correct? Explain why or why not.
- Devin takes his turn. His marker is on the 1, and he spins a 4 and a –3. Is it possible for Devin to get to one of the winner spaces (at 11 and –11) with these numbers? Explain your answer.
- Gavin now has his marker at 12, and he spins a –3 and a –2. Gavin is wondering if he can win on this turn. Can he? Explain your answer.
- Mark is currently at −14 and spins a −3 and a −1. He sees a way to win. How can he do this? Is there more than one way? Explain your answer.
3-81. Roger went home to play the Tug-o-War game with his older brother, Hank. Hank looked at the spinners, thought for a bit, and then told Roger that the game is flawed because you cannot get all of the integers from −10 to +10. Roger wondered if Hank was right.
Are there any integers from −10 to +10 that you cannot get using any of the operations with the results of a spin on each spinner? Do you think that this would make the game unfair or flawed? Work with your team to build a convincing argument that demonstrates whether or not Hank’s claim is true.
Assignment: 3.2.5 Homework
Formative Asmnt 3-2-5 P3-80 Resource Page
[/expand]
[expand title=”How can I divide?”]
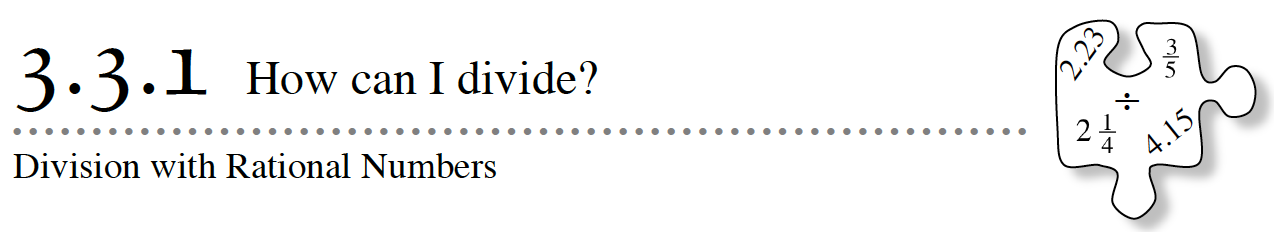
A fraction is really just a symbolic representation of the quotient (answer to a division problem) of two quantities. The fraction 
really means 3 ÷ 4 = 0.75. In this lesson, you will work with dividing fractions, positive and negative mixed numbers, and decimals.
3-87. A rational number is any number that can be written as a quotient or fraction of integers, that is, in the form 
, with the denominator not equal to zero.
- What mathematical operation does a fraction represent?
- Represent each division problem below as a fraction.
- 2 ÷ 8
- 72 ÷ 5
- 51 ÷ 94
- Why do you think that the denominator of a fraction cannot equal zero?
- When would it be most useful to use a fraction to find the answer to a division problem instead of using long division?
3-88. Think about how you rewrote the division problems above as fractions. This can also be done with negative rational numbers (fractions). Is −
different from 
, 
, and 
? Discuss this with your team and decide whether these rational numbers are the same or different. Be prepared to share your answers with the class.
3-89. Huy, Madison, and Ramona were working the following problem and each began her work differently.
÷
Your Task:Work with your team to make sense of each student’s approach to the problem. Then use each of the three approaches to do the following two problems.
÷ 2÷ 3-90. You have seen three methods for dividing fractions: a diagram, finding a common denominator, and using a Super Giant One. If you need more review of these methods, look at the Math Notes box that follows this lesson. Decide with your team which method you will use for each part (a) and (b) below. Write the problem as a fraction division problem, solve it, and explain what each part of the division problem represents in each story.
- Gerard loves to cook. His aunt visited Switzerland and brought him back four pounds of Swiss chocolate. Gerard’s favorite cookie recipe takes 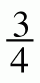of a pound of chocolate. How many batches of the chocolate cookie recipe can Gerard make using all the chocolate that he has?
- Lauren was bringing food to a party. She bought a 4-foot sub sandwich and cut it into servings that were each 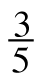of a foot long. How many servings did she get if she used the whole 4-foot sandwich?
3-91. Use any strategy to solve the following division problems.
- −2
÷
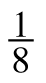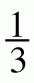
- (−1) ÷ (−
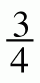) - How are the sign rules for simplifying expressions with rational numbers similar to the sign rules for simplifying expressions with integers?
3-92. Stellica wants to find the quotient (answer to a division problem) 0.016 ÷ 0.25, but she is not sure how to divide decimals. She decided to rewrite the numbers as fractions.
- With your team, rewrite 0.016 ÷ 0.25 using fractions and use what you know about dividing fractions to find an answer that is one fraction.
- Stella knew that her teacher would want her to write the answer as a decimal, since the original problem was written with decimals. Convert your answer from part (a) to a decimal.
- Find the quotient 2.38 ÷ 0.04.
Assignment: 3.3.1 Homework
[/expand]
[expand title=”Why would I use decimals?”]
Today you will review and practice working with decimals. While you might usually use a calculator when dividing decimals, it is important that you understand how decimal division works. This way, when you encounter problems that involve both decimals and variables, you will be able to simplify expressions and manipulate the symbols correctly and efficiently. Today’s problems will help you extend what you know about fraction division to make sense of decimal division.
For today’s lesson, you may only use your calculator to check answers that you have first calculated by hand or when you are specifically directed to use it.
3-98. SPACE FOR SPACERS
Mr. Garcia needs to cut short pieces out of a 16-foot-long board to use as spacers in the wall of his new house. The pieces he needs for spacers must be 9 inches long. Without using your calculator, how would you determine how many such spacers could be cut from Mr. Garcia’s board?
3-99. Sloan is a fraction wizard and prefers to convert all numbers in any problem to fractions, but her teacher insists that she be able to do Mr. Garcia’s problem with decimals as well. Sloan knows that 9 inches is the same as of a foot, so she first wrote Mr. Garcia’s problem as 
.
“I suppose I could use decimals,” Sloan moaned. “I know the decimal equivalent for is 0.75.” And then she wrote the division as
.
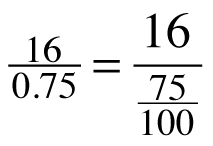“Oops… I’m just back to fractions. What do I do now?” Sloan asked her teammates.
- Which Giant One would you have to multiply by to change Sloan’s fraction to a fraction with integers? Multiply by that fraction and record your answer.
- Decide with your team if “1600 divided by 75” is the same problem as
“16 divided by 0.75.” Why or why not? - Write a note to Sloan explaining your answer to part (a). Include the steps to complete Sloan’s work using the long division algorithm to divide
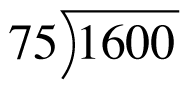. Show all your work. Write the answer in decimal form.
3-100. Many people have difficulty locating the decimal point in the answer to a problem like 
. Use your answer to part (b) of problem 3‑99 to rewrite with whole numbers. Then find the answer using long division. Do not use a calculator.
3-101. Use your calculator to do the following problems quickly. As you do them, write an equation for each problem on your paper.
- 3 divided by 4
- 1.5 divided by 0.25
- 15 divided by 2.5
- 30 divided by 40
- 0.003 divided by 0.004
- 0.15 divided by 0.025
- divided by
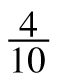
- 0.0015 divided by 0.00025
What do you notice about these problems? How can you explain the similarities and differences?
3-102. Eloise wants to divide 0.07 ÷ 0.4 and thinks she sees a shortcut. “Can I just divide 7 ÷ 4?” she wonders.
- What do you think? Will her shortcut work? Discuss this with your team and be prepared to explain why or why not.
- Determine the answer to 0.07 ÷ 0.4, and show how you found your answer.
3-103. Set up the division problems below with whole numbers, as shown in the previous problem, to help you solve the problems below. Show all of your work.
3-104. Tom’s kitchen is 12.5 feet wide. He wants to tile the floor with 0.75-foot-wide tiles. How many tiles will be needed for one row of tiles that extend across the length of the floor? Write and solve a division problem and explain what each part of the problem represents in the story.
3-105. For each problem below, write and solve a story problem. Be sure to explain what each part of the division problem represents in the story. Be ready to share your stories with the class.
- 11.25 ÷ 0.4
- 4.3 ÷ 0.25
3-106. LEARNING LOG
In your Learning Log, explain how to find the answer to a division problem with rational numbers. Title this entry “Division with Rational Numbers” and label it with today’s date.
Assignment: 3.3.2 Homework
[/expand]
[expand title=”How can I simplify numerical expressions?”]
Remember when operations with numbers were simple? In elementary school, you learned to add, subtract, multiply, and divide whole numbers. As you have seen, there is a lot to consider when operating with different kinds of numbers. In this lesson, you will put together much of your understanding of operations with integers and simplifying numerical expressions to draw conclusions about order and grouping of operations.
3-112. Juno was working on simplifying the expression 24 + 3 +(−4) + 7. “I know!” he exclaimed. “It must be equal to 30, because 20 plus 10 is 30.”
- Is Juno correct? Is the value of the expression 30?
- How could Juno have found 20 and 10 in this expression? Discuss this with your team and be prepared to share your ideas with the class.
3-113. In problem 3-112, Juno used his understanding of two different properties: the Commutative Property of Addition and the Associative Property of Addition. The Commutative Property of Addition allows Juno to rearrange 24 + 3 + (−4) + 7 into a different order, such as 24 + (−4) + 3 + 7. The Associative Property of Addition allows him to group numbers in different ways, so instead of adding from left to right, he can add in two groups and then combine them like this: (24 + (−4)) + (3 + 7) = 20 + 10 = 30.
- Talk with your team about the Commutative Property of Addition. Does it work for other operations? In other words, can multiplication, division, and subtraction be done in any order? Be ready to explain your ideas to the class.
- Talk with your team about the Associative Property of Addition. Does it work for other operations? In other words, can multiplication, division, and subtraction be done in any grouping? Be ready to explain your ideas to the class.
3-114. Consider expressions involving addition and subtraction, such as 7 − 2 + 4.
- Work with your team to calculate the value of this expression. Be prepared to explain your method to the class.
- Does the grouping matter? In other words, is (7 − 2) + 4 the same as 7 − (2 + 4)? Explain.
- Does order matter? In other words, is 7 − 2 + 4 the same as 2 − 7 + 4? Explain.
- In expressions that involve addition and subtraction, in what order should those operations be calculated? Consider the following expressions to help you think about this.
- 10 − 2 + 4
- 3 − 5 − 2 + 6
- 7 − 3 − 2
3-115. Juno has another idea. “Wait!” he says. “Can’t subtraction be rewritten using addition? Since order doesn’t matter when we add, can’t we just rewrite the subtraction as addition so we can use any order?”
Discuss Juno’s idea with your team and then rewrite each of the following expressions so that each one involves only addition. Then use the fact that the numbers are all being added and the order can be changed to find a way to simplify each expression efficiently.
- 17 − 4 − 11 + 15
- 2 − 2 · 3 − 4 − 2(−4)
3-116. Maria and Jorge were trying to simplify the expression (−
) · 1· (−). Maria started by rewriting 1as 
. Her work is below.
Jorge had a different idea. He multiplied (−) · (−) first.
- Simplify the expression 1· (−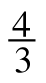) · (−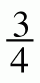) using Jorge’s method. Is your answer equal to Maria’s?
- Jorge used the Commutative Property of Multiplication. Why might Jorge have decided to multiply (−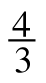) · (−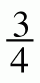) first?
- In a multiplication problem, the factors can be grouped together in different ways. This is called the Associative Property of Multiplication. Use this property and show that (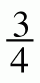·) · (−2) and 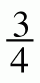·( · (−2)) are equivalent.
- Simplify each expression. First decide if you want to group some factors together.
- (−9) ·
· - −
·
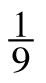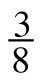
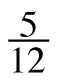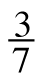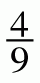
· - −8.1 · 5 · 2
- (−9) ·
3-117. Additional Challenge: Use each integer –6, 2, –3, and 1 once with any of the four operations or parentheses to make:
a. The largest possible answer.
Zero or the closest number to zero.
The smallest possible answer.
3-118. You have learned several methods for solving problems with decimals and fractions. As you solve these problems, clearly show all of your work. Also show the connection between the parts of the word problem and the parts of your math problem. Be sure to explain what your answer represents in the story.
Tinaya worked 42.2 hours last week. If she is paid $15.65 an hour, what was her total pay (before taxes) for the week?
Joe has a medicine bottle with 6 oz of liquid medicine in it. If each dose is oz., how many doses does Joe have if he will use all the medicine?
If the temperature changes –2.6 degrees each hour for 8.2 hours, how much does the total temperature change?
Jack and some friends climbed Long’s Peak in Rocky Mountain National Park. Then he and his friends started down the mountain, losing 1515 feet of elevation each hour. They hiked for 6
hours to get back down to the parking lot. How many feet of elevation did they lose?
Mr. Solomon, the art teacher, has 49.6 pounds of clay. If he gives every student 1.6 pounds of clay and has none left, how many students are in his class?
3-119. Your teacher will assign you one of the situations from problem 3-118 to make a stand-alone poster. A stand-alone poster means explaining all your thoughts in writing because you will not be explaining it orally.
On your poster, be sure to write the original story problem, write the math problem, and show how to solve the problem two different ways. Using drawings or words, show what each part of the math problem and the answer represents.
Assignment: 3.3.3 Homework
[/expand]