Quadratic Equations

[expand title=”Working with polynomials”]

  • PH 8-1
    • Degree of polynomial
    • Adding polynomials
    • Subtracting polynomials
    • Assignment: P. 373-374 (1-49 odd)
  • PH 8-2
    • Multiplying and dividing polynomials
    • Factoring out a common factor
    • Assignment: P. 377-378 (1-31 odd, 35-39 odd)

[/expand]

[expand title=”FOIL”]

  • PH Activity Lab P.380
    • Algebra blocks
    • Exercises 1-6
  • PH 8-3
    • Multiplying two binomials
    • Using the distributive property
    • FOIL
    • Assignment: P. 383-384 (1-37 odd, 51)

[/expand]

[expand title=”Factoring quadratics (trinomials)”]

  • PH 8-5
    • Factoring positive and negative trinomials of the form x ^{2}+bx+c
    • Assignment: P. 397 (1-29 odd)
  • PH 8-6
    • Factoring trinomials of the form ax ^{2}+bx+c
    • Assignment: P. 401-402 (1-31 odd)
  • PH 8-7
    • Factoring special special cases
    • Perfect squares
    • Difference between squares
    • Assignment: P. 407 (1-37 odd)
  • PH 8-8
    • Factor by grouping
    • Assignment: P. 413 (1-37 odd)

[/expand]

[expand title=”Quadratics Quiz”]

 

[/expand]

[expand title=”Square Roots”]

  • PH 9-3
    • Square roots: Principal square root and negative square roots
    • Rational and irrational square roots
    • Estimating square roots
    • Assignment: P. 442-443 (1-47 odd)

[/expand]

[expand title=”Solving Quadratics”]

  • PH 9-4
    • Finding x-intercepts – Roots or Zeros
    • Assignment: P. 447-448 (1-21 odd, 35, 37)
  • PH 9-5
    • Factoring to solve quadratic equations
    • Using the zero-product property
    • Assignment: P. 454 (1-33 odd)

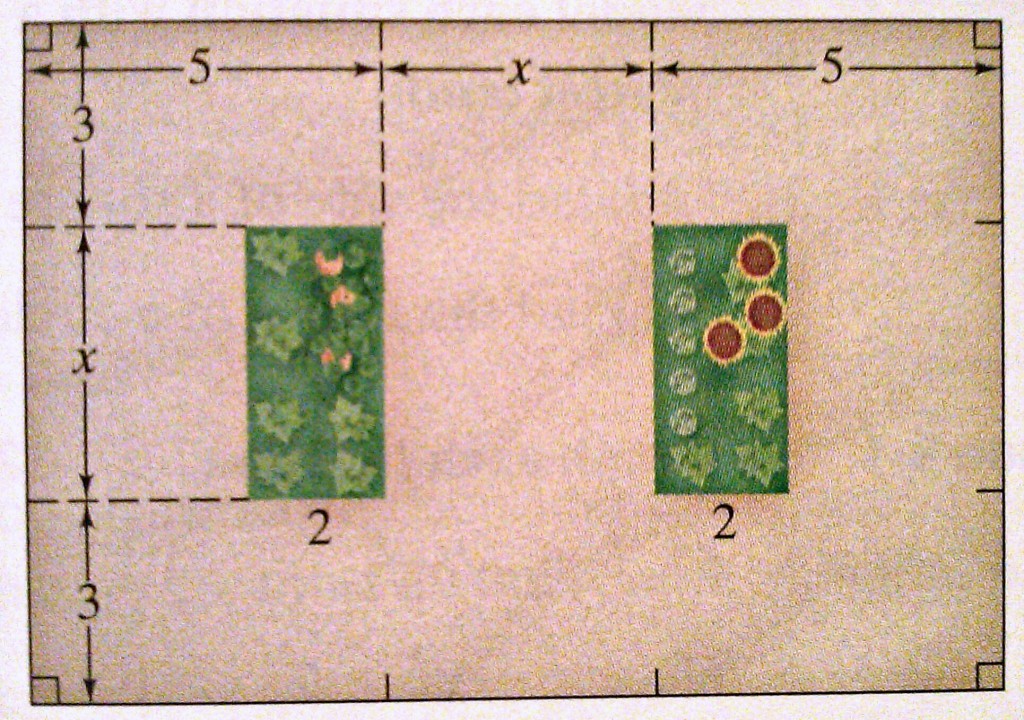
Challenge

You are building a rectangular patio with two rectangular openings for gardens. You have 124 one-foot-square paving stones. Use the diagram below, what value of x would allow you to use all of the stones?

 

Solving-Quad-Rectangular-patio

 

 

[/expand]

[expand title=”Completing the Square”]

  • PH 9-6
    • Completing the square
    • (\frac{b}{2}) ^{2}
    • P. 458-459 Ex 2-4
    • Assignment: P. 460 (1-35 odd)

Small Steel Frame

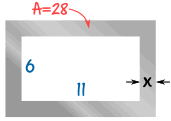
Your company is going to make frames as part of a new product they are launching.

The frame will be cut out of a piece of steel, and to keep the weight down, the final area should be 28 cm2

The inside of the frame has to be 11 cm by 6 cm

What should the width x of the metal be?

[/expand]

[expand title=”Deriving the quadratic equation from standard form”]

Derive Quadratic Formula

 

Now try with \chi ^{2}+6\chi-7=0

 

  • PH 9-7
    • Quadratic Formula
    • Derivation from standard form of a quadratic
    • P. 464-465 Ex 1-3
    • Assignment: P. 466-467 (1-33, 37)

[/expand]

[expand title=”Using the quadratic equation an the Discriminant”]

  • PH 9-8
    • Using the discriminant
    • b ^{2}-4ac
    • Quadratic equations can have 1, 2, or zero real solutions. The discriminant allows us to determine the number of possible solutions before we solve.
    • If the discriminant > 0, there are two real solutions
    • If the discriminant = 0, there is one real solution.
    • If the discriminant < 0, there are no real solutions.
    • Example 1-3
    • Assignment: P. 472-473 (1-31 odd)

[/expand]

[expand title=”Application of quadratic equations”]

Answer – Quadratic word Problems II

SolvingQuadratics-Re-engagement

Garden Deck Challenge

Triple the fun with quadratics

Quadratic Word Problems – Mix with Number Theory

[/expand]

Assessment