Concept 8 – Expressions and Equations

Week 23 – Comparing Expressions

6-2. Using your Expression Comparison Mat, build the two expressions below using algebra tiles.  Find a way to determine which side is greater, if possible.  Show your work by sketching it.  Be ready to share your conclusion and your justification. Explore using the 6-2 tiles (CPM).

pic

6.1.1 Homework

6-3. MORE COMPARING EXPRESSIONS – Is one expression greater? Consider how you were able to compare the expressions in the previous problems.  When is it possible to remove tiles to compare the expressions on the mats?  In this problem, you will work with your team to identify two different “legal moves” for simplifying expressions. Build the mat below using algebra tiles  and simplify the expressions.  Record your work by drawing circles around the zeros or the balanced sets of tiles that you remove in each step on the Lesson 6.1.1B Resource Page.  Which expression is greater? pic  
6-4. There are two kinds of moves you could use in problem 6-3 to simplify expressions with algebra tiles.  First, you could remove matching (or balanced) sets of tiles from both sides of the mat.  Second, you could remove zeros.  Both moves are shown in the figures below.  Justify why each of these moves can be used to simplify expressions.
6-5. WHICH SIDE IS GREATER? For each of the problems below, use the Expression Mat and:
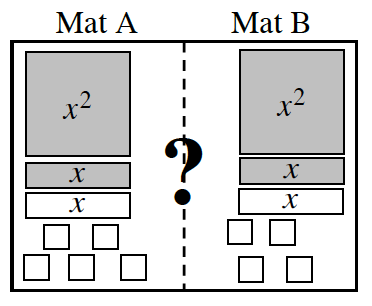
  • Build the two expressions on your mat using algebra tiles.
  • Write an expression for each side below the mats for parts (a) through (d) OR draw the tiles in the space given on the resource page for parts (e) and (f).
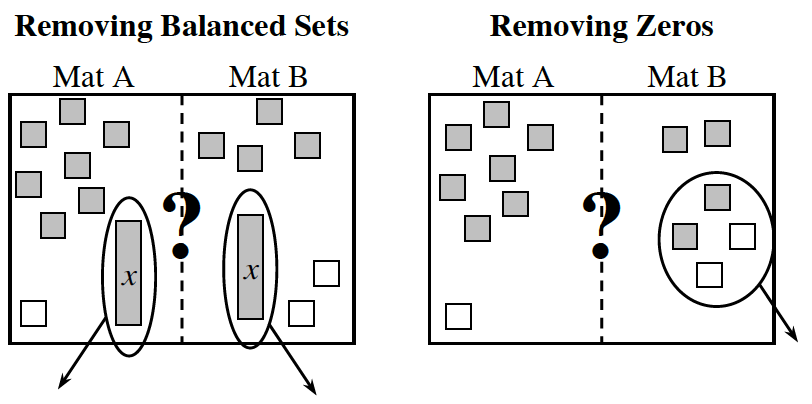
  • Use legal moves to determine which mat is greater, if possible.  Record your work by drawing circles around the zeros or the balanced (matching) sets of tiles that you remove in each problem.pic
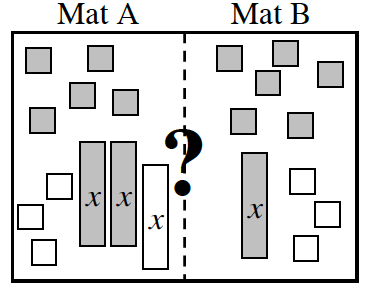
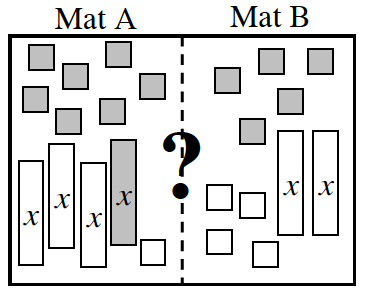
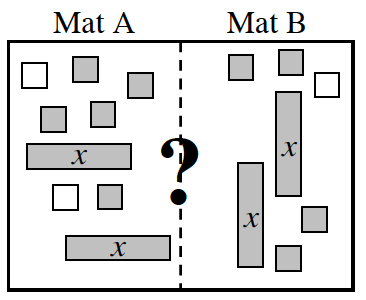
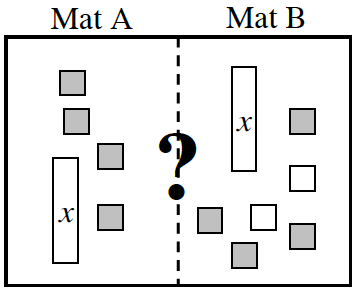
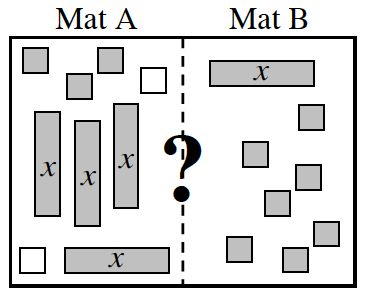
    5. Mat A: 3x − 4 − 2 Mat B: 3(x − 1)
    6. Mat A: 5 + (−3x) + 5x Mat B: x2 + 2x + 1 − x2
6-13. WHAT HAPPENED? When Ignacio and Oliver compared the expressions in part (d) of problem 6-12, they could not figure out which side was greater. pic
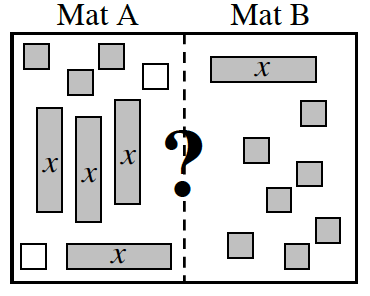
  1. Is it always possible to determine which side of the Expression Comparison Mat is greater (has the greater value)?  Why or why not?  Be prepared to share your reasoning.
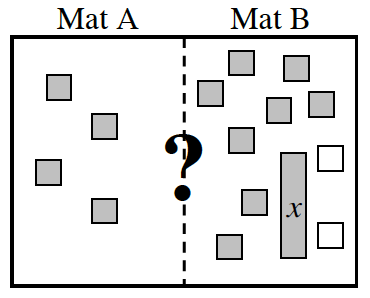
  2. How is it possible for Mat A to have the greater value?
  3. How is it possible for Mat B to have the greater value?
  4. In what other way can Mat A and B be related?  Explain.
6-12. Use the simplification strategies of removing zeros and simplifying by removing matching pairs of tiles to determine which side is greater, if possible.  Lesson 6.1.2 Resource Page.pic
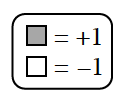
  2. Mat A: 2(x + 3) − 4 Mat B: 3x + (−1) − x + 4

Week 24 – Solving Equations with Tiles

6-48. CHOOSING A PRICE PLAN Sandeep works at a bowling alley that currently charges players $3 to rent shoes and $4 per game.  However, his boss is thinking about charging $11 to rent shoes and $2 per game. a. If a customer rents shoes and plays two games, will he or she pay more with the current price plan or the new price plan?  Show how you know. b. If the customer bowls 7 games, which price plan is cheaper?   6-48Bowling Alley Plans - WB
6-49. WILL THEY EVER BE EQUAL? Sandeep decided to represent the two price plans from problem 6-48 with the expressions below, where  x  represents the number of games bowled. Then he placed them on the Expression Comparison Mat shown at right. pic
Original: 4x + 3                   New price: 2x + 11




 




    a. Are his expressions correct?  Find both the original and new prices when x = 2 and then again when x = 7 games.  Did you get the same prices as you found in problem 6-48? b. Sandeep then simplified the expressions on the mat.  What steps did Sandeep take to simplify the mat to this point?
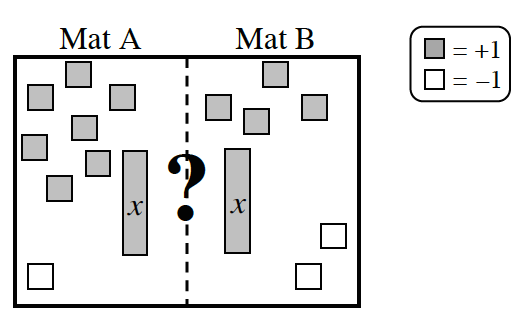
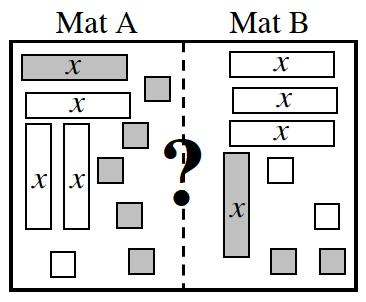
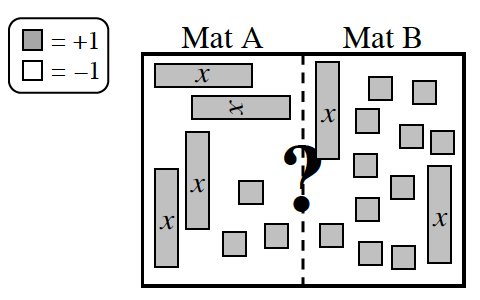
6-14. Ignacio and Oliver are playing another game with the algebra tiles. pic After they simplify two new expressions, they are left with the expressions on their mats shown at right.  They could not tell which part of the mat is greater just by looking.  

a) One way to compare the mats is to separate the x‑tiles and the unit tiles on different sides of the mat.  Work with your team to find a way to have only x‑tiles on Mat A.  Make sure that you are able to justify that your moves are legal.  


b) Using the same reasoning from part (a), what would you do to have only the variable on Mat B in the Expression Comparison Mat at right?pic



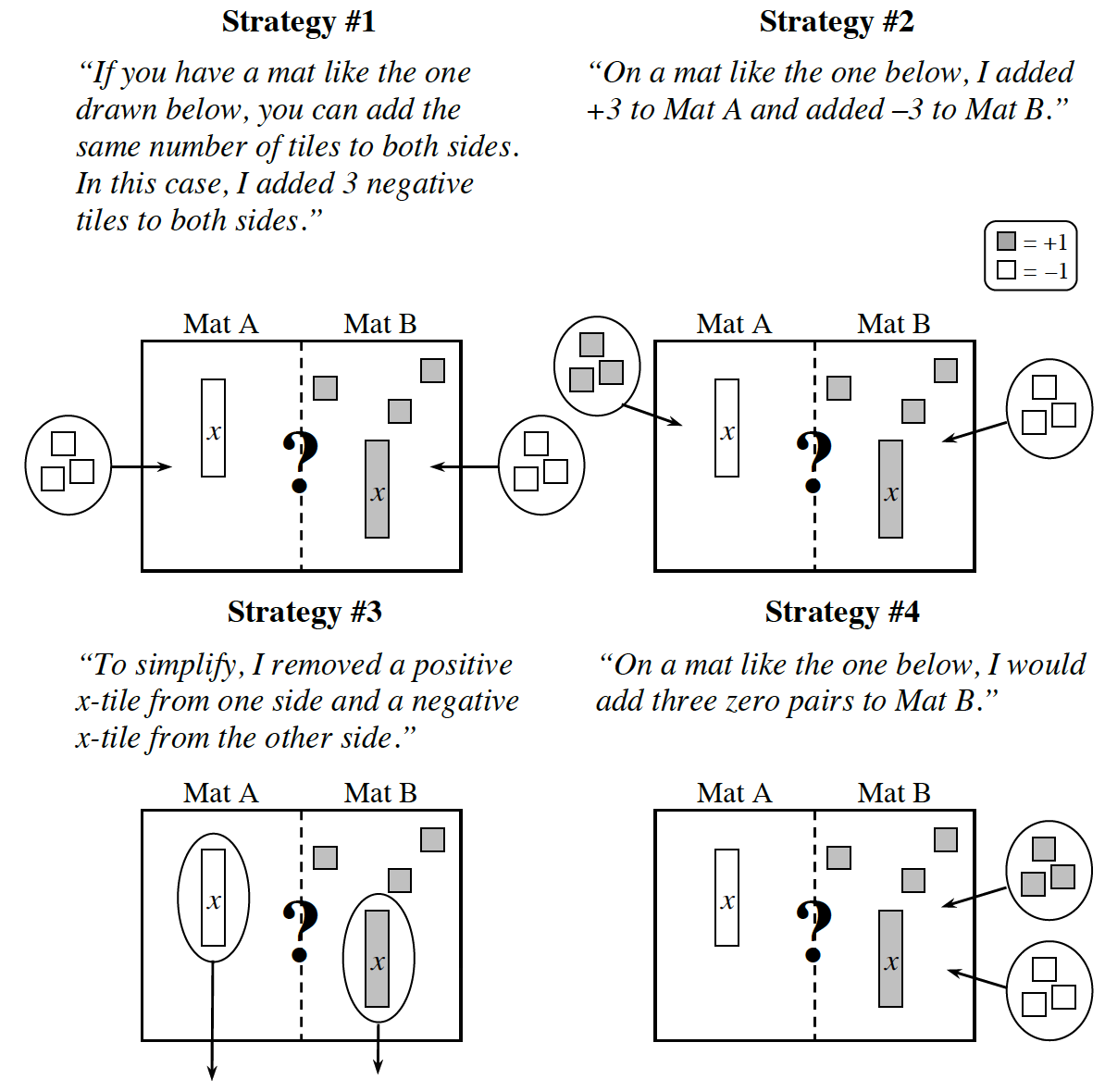
6-14 Moving Tiles - WB
6-15. Ignacio and Oliver are trying to decide if there are other ways to change expressions on the Expression Comparison Mat without affecting which side is greater.  They have invented some new strategies and described them below.

Your task: For each of the moves below:
  • Build the Expression Comparison Mats on your paper.
  • Follow each set of directions for the mat shown in each strategy below.
  • Do you think it was a legal move?


6-15 Adding tiles to both sides

Solve Eq Alg Tiles #1

Solve Eq Alg Tiles #2

Solve Eq Alg Tiles #3

Using Algebra Tiles to Solve Equations Algebraically #3

Week 25 – Solving with Tiles Continued

6-50. SOLVING FOR X When the expressions on each side of the comparison mat are equal, they can be represented on a mat called an Equation Mat.pic Now the “=” symbol on the central line indicates that the expressions on each side of the mat are equal.
a. Draw the equation mat in your notebook.
b. Then, record the original equation represented on your Equation Mat.
c. Simplify the tiles on the mat as much as possible.  Record what is on the mat after each legal move as you simplify each expression.  What value of  x  will make the expressions equal?

6-50 Equation Mat WB
6-51. Amelia wants to solve the equation shown on the Equation Mat at right.  After she simplified each expression as much as possible, she was confused by the tiles that were left on the mat.pic a. What was Amelia’s original equation?

b. Remove any zero pairs that you find on each side of the Equation Mat.  What happens?

c. What is the solution to this equation?  That is, what value of  x  makes this equation true?  Explain your reasoning.
6-52. Amelia's Friend was also trying to solve the following equation but needs help.
2x + 2 + (−3) = 5x + 8.
Help her find the value of  x  that makes these expressions equal.  Be sure to:
a. Record the expressions in your notebook.
b. Draw the mat on your paper.
c. Simplify the mat to help you figure out what value of  x  makes this equation true.  Be sure to record your work in symbols on your paper.

Week 26 – Solving Equations Algebraically

Assignment: Two-Step Equations With Integers
What do you do when there are variables on both sides of an equation?
Examples:
  • x + 1 = 2x – 5
  • 3x + 6 = – x + 2
  • 6x + 6 = – 4x + 86
  • 7x + 1 = 2x + 41
Exercise 1
1.)    5x + 8 = 57 – 2x 2.)    7x + 9 = 45 + 3x
3.)    x + 7 = – 6x + 21 4.)    – 4x + 1 = 13 – 3x

Assignment: Multi-step variables on both sides
Your brother is going to college, so you no longer have to share a bedroom. You decide to redecorate a wall by hanging two new posters on the wall. The wall is 14 feet wide and each poster is four feet wide. You want to place the posters on the wall so that the distance from the edge of each poster to the nearest edge of the wall is the same as the distance between the posters, as shown in the diagram below. Determine that distance. 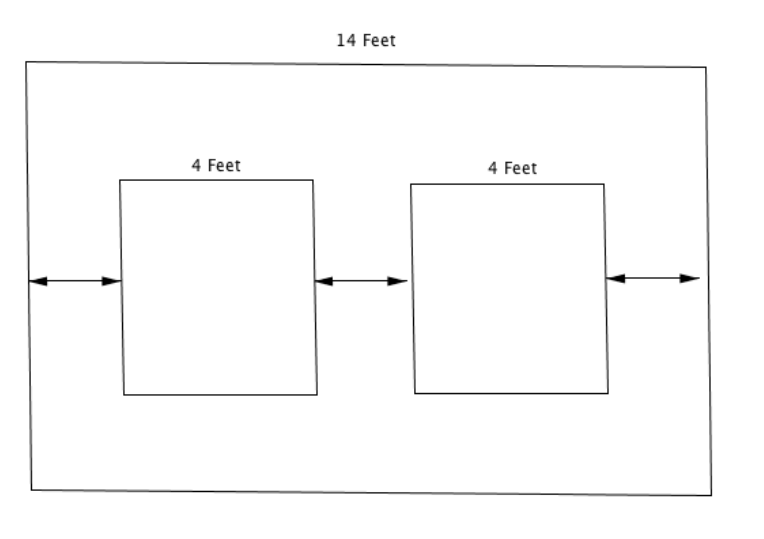7.3.7.OpenExercise
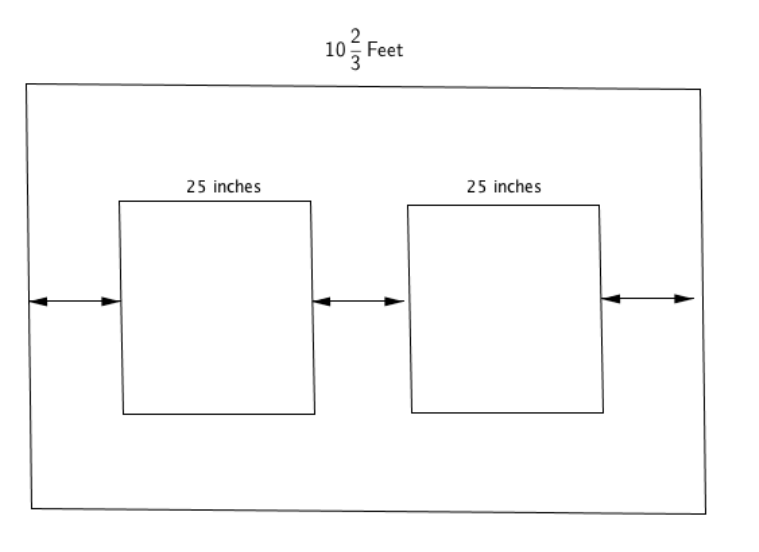Your parents are redecorating the dining room and want to place two rectangular wall sconce lights that are 25 inches wide along a 10 foot, 8 inch wall, so that the distance between the lights and the distances from each light to the nearest edge of the wall are all the same. Design the wall and determine the distance. 7.2.7.Exercise1 Let the distance between a light and the nearest edge of a wall be x ft. Write an expression in terms of x for the total length of the wall, and then use the expression and the length of the wall given in the problem to write an equation that can be used to find that distance.

Introduction to Solving Equations

Solving Equations Alg 1.3

Solving Equations Alg 1.2

Solving Two Step Equations Maze-1

Two Step Equations Maze 2

Solving One and Two Step Equations Mazes

Multi-Step Equations Mystery Activity Scavenger Hunt Clue

Solving Inequalities

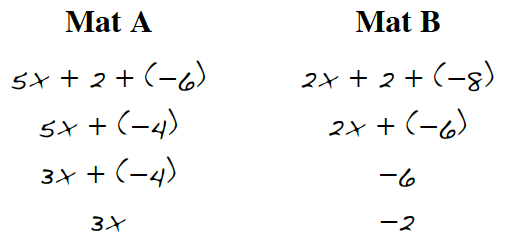6-23. Maria has been recording her work to see which side of an Expression Comparison Mat is greater, but she has been called away.  Garth looked at her work, but he cannot figure out what Maria did to get from one step to another. picLook at Maria’s work above and help Garth by building the expressions on your mat using algebra tiles and simplifying them.  Write him a note explaining what Maria did to get from one step to another.
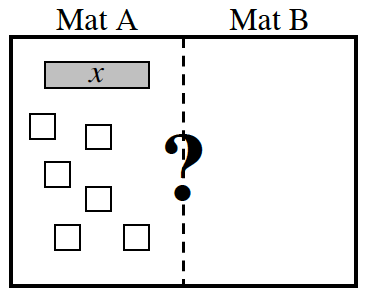
6-24. Compare the expressions 2 + 2x + (−3) and 2x + (−4) + 1 using algebra tiles.  Use Maria’s method of recording to show your steps.  Make sure you record each step so that your teacher or others could see what you did on your Expression Comparison Mat. a. Which mat is greater? b. Use symbols such as to show the relationship between the final expressions on Mat A and Mat B.
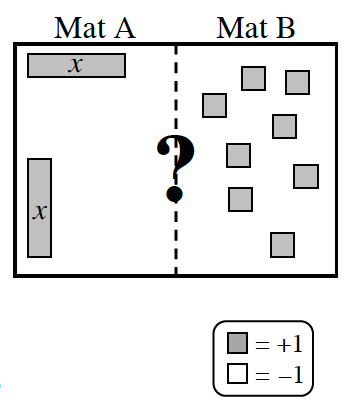
6-25. Maria and Garth were playing a game with the algebra tiles.  They each grabbed a handful of tiles and put them on the Expression Comparison Mat at right to see whose side had greater value.  pic Maria said, “I have Mat A and my side has more value.”  Garth, who had Mat B, disagreed with her.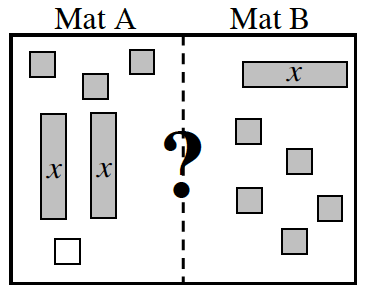 a. Write expressions for Mat A and Mat B. b. Work with your team to simplify the expressions on the Expression Comparison Mat while carefully recording your work for each step on your paper with symbols.  Can you tell whose side is greater?  Why or why not? c. With your team, find at least four values for  x  that would make the expression on Maria’s side (Mat A) greater than the expression on Garth’s side (Mat B).  Be prepared to share your values with the class. d. Any value for  x  that makes Mat A greater than Mat B is a solution to the inequality 2x + 3 + (–1) > x + 5.  This is read, “Two  x  plus three plus negative one is greater than  x  plus five.” 
6-26. Karla had a hard time keeping track of all of the solutions to the inequality in problem 6-25 in her head.  She decided to try to organize her answers.  First she needed to know more about the problem. a. Is there a greatest number that is a solution?  Discuss this question with your team and be prepared to share your ideas with the class. b. Is there a smallest number that is a solution?  Again, be prepared to share your team’s thinking with the class. c. What is special about the point where the solutions end?  (This number is called the boundary point.)  In other words, what relationship does this number have to the two expressions being compared? d. Karla was tired of listing so many solutions and wanted a quick way to show all of the solutions to this inequality.  She decided to draw a number line like the one below.

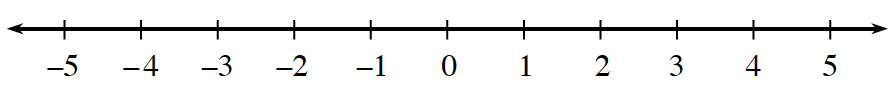
On your own paper, draw a number line such as the one above then follow your teacher’s directions to represent the answer to this question on your number line.
6-27. Now consider the inequality 2x + 5 < 3, which can be read “Two  x  plus five is less than 3.” Build the inequality on your Expression Comparison Mat using algebra tiles and record each step on your paper using symbols.  Work with your team to describe the least and greatest solutions to the inequality and draw your solution on a number line.  Be prepared to justify your ideas. Assignment: 6.1.3 Homework [/expand]  
6-35. Jerry and Ken were working on solving the inequality 3x − 1 < 2x.  They found the boundary point and Ken made the number line graph shown below.

pic

Jerry noticed a problem.  “Doesn’t the line at the bottom of the < symbol mean that it includes the equal part?  That means that x = 1 is also a solution.  How could we show that?” “Hmmm,” Jerry said.  “Well, the solution x = 1 would look like this on a number line.  Is there a way that we can combine the two number lines?”

pic

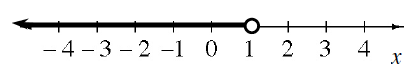
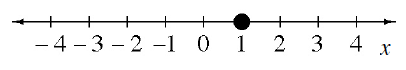
Discuss this idea with your team and be prepared to share your ideas with the class. pic6-36. The diagram at right shows three possible ways to represent inequality statements.  Review the meanings of the inequality symbols >, <, >, and < with your team.  Then, generate the two missing representations from each inequality described in parts (a) through (c) below.
  1. x < − 1
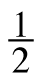
  2. x is greater than or equal to two.
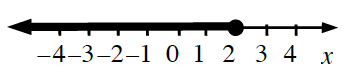
6-37. WHEN IS THE BOUNDARY POINT INCLUDED? Represent the solution for each of the variables described below as an inequality on a number line and with symbols. The speed limit on certain freeways is 65 miles per hour.  Let  x  represent any speed that could get a speeding ticket. You brought $10 to the mall.  Let  y  represent any amount of money you can spend. To ride your favorite roller coaster, you must be at least five feet tall but less than seven feet tall.  Let  h  represent any height that can ride the roller coaster.
6-38. Ellie was still working on her dollhouse.  She has boards that are two different lengths.  One long board is 54 inches.
  1. The length of the short board is unknown.  Ellie put three short boards end-to-end and then added her 12-inch ruler end-to-end.  The total length was still less than the 54‑inch board.  Draw a picture showing how the short and long boards are related.
  2. Write an inequality that represents the relationship between the short boards and 54 inches shown in your diagram in part (a).  Be sure to state what your variable represents.
  3. What are possible lengths of the short board?  Show your answer as an inequality and on a number line.
6-39. Jordyn, Teri, and Morgan are going to have a kite-flying contest.  Jordyn and Teri each have one roll of kite string.  They also each have 45 yards of extra string.  Morgan has three rolls of kite string plus 10 yards of extra string.  All of the rolls of string are the same length.  The girls want to see who can fly their kite the highest.
  1. Since Jordyn and Teri have fewer rolls of kite string, they decide to tie their string together so their kite can fly higher.  Write at least two expressions to show how much kite string Jordyn and Teri have.  Let  x  represent the number of yards of string on one roll.
  2. Write an expression to show how much kite string Morgan has.  Again, let  x  be the number of yards of string on one roll.
  3. How long does a roll of string have to be for Jordyn and Teri to be able to fly their kite higher than Morgan’s kite?  Show your answer as an inequality and on a number line.
  4. How long does a roll of string have to be for Morgan to be able to fly her kite higher than Jordyn and Teri’s kite?  Show your answer as an inequality and on a number line.
  5. What length would the roll of string have to be for the girls’ kites to fly at the same height?
6-40.Additional Challenge: Travis loves trains!  Today he is beginning a train ride from Madison, Wisconsin all the way to Seattle, Washington. Shortly after the train left the station in Madison, Travis fell asleep.  When he woke up, it was dark outside and he had no idea how long he had been asleep.  A fellow passenger told him they had already passed La Crosse, which is 135 miles from Madison.  If the train travels at an average speed of 50 miles per hour, at least how long has Travis been asleep?  Represent this problem with an inequality and then solve it.  

Assignment: 6.1.2 Homework

Assignment: 6.1.4 Homework

6-64 Solving with tiles Practice – WB

 

6-53.Additional Challenge: Try the number puzzle below. Pick any number, add 20, multiply your answer by 2, and subtract 30 from the result.  Then, divide your answer by 2 and subtract your original number. a. What is the result? b. Try it with several different numbers.  Is the result the same every time? c. Using a variable (such as  n) to represent the starting number, show why the final result is always the number 5.

Assignment: 6.2.1 Homework [/expand]

[expand title=”How do I know that it is correct?”] Sometimes a lot can depend on the solution of a problem.  For example, when businesses calculate the cost of packaging and shipping a product, they need to come up with an accurate value.  If they miscalculate by only $0.01 per package but ship one million packages per year, this small miscalculation could be costly. Solving a problem is one challenge.  However, once it is solved, it is important to have ways to know whether the solution you found is correct.  In this lesson, you will be solving equations and finding ways to determine whether your solution makes the equation true.

6-60. Chen’s sister made this riddle for him to solve: “I am thinking of a number.  If you add two to the number then triple it, you get nine.” a. Build the equation on an Equation Mat using algebra tiles.  What are two ways that Chen could write this equation? b. Solve the equation and show your work by writing the equation on your paper after each legal move. c. When Chen told his sister the mystery number in the riddle, she said he was wrong.  Chen was sure that he had figured out the correct number.  Find a way to justify that you have the correct solution in part (b).

6-61. Now solve the equation 4(x + 3) = 8.  Remember to:

  • Build the equation on your Equation Mat with algebra tiles.
  • Simplify the equation using your legal moves.
  • Record your work on your paper.
  • Solve for  x.  That is, find the value of  x  that makes the equation true.

6-62. CHECKING YOUR SOLUTION When you solve an equation that has one solution, you get a value for the variable.  But how do you know that you have done the steps correctly and that your answer “works”? a. Look at your answer for problem 6-61.  How could you verify that your solution is correct and convince someone else?  Discuss your ideas with your team. b. When Kelly and Madison compared their solutions for the equation 2x − 7 = −2x + 1, Kelly got a solution of  x = 2 and Madison got a solution of  x = −1.  To decide if the solutions were correct, the girls decided to check their answers to see if they made the expressions equal. Finish their work below to determine if either girl has the correct solution.

pic

c. When checking, Kelly ended up with −3 = −3.  Does this mean that her answer is correct or incorrect?  And if it is correct, does this mean the solution is x = −3 or  x = 2?  Explain.

d. Go back to problem 6-61 and show how to check your solution for that problem.

pic

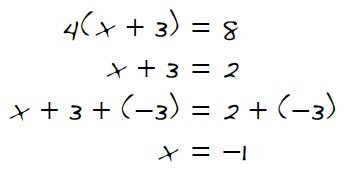
6-63. Kelly solved the equation  4(x + 3) = 8 from problem 6-61.  Her work is shown at right. a.  If 4(x + 3) = 8, does x + 3 have to equal 2?  Why? b. What did Kelly do to remove the 3 unit tiles from the left side of the equation?  Does this move affect the equality? c. If Kelly were solving the equation 3(x − 5) = 9, what might her first step be?  What would she have after that step?  You may want to build this equation on an Equation Mat to help make sense of her strategy.

Assignment: 6.2.2 Homework [/expand]

[expand title=”How can I record it?”] In this lesson, you will continue to improve your skills of simplifying and solving more complex equations.  You will develop ways to record your solving strategies so that another student can understand your steps without seeing your Equation Mat.  Consider these questions as you work today:

How can I record the steps I use to solve?
How can I record what is on the Equation Mat after each step?

6-71. Gene and Aidan were using algebra tiles to solve equations.  Aidan was called away. Help Gene finish by completing the table shown below and on the Lesson 6.2.3 Resource Page.

6-72. Aidan was frustrated that he needed to write so much when solving an equation.  He decided to come up with a shortcut for recording his work to solve a new equation. 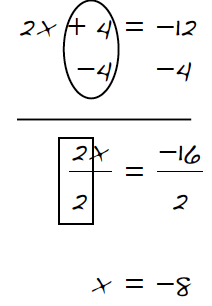picAs you look at Aidan’s recording at right of how he solved 2x + 4 = −12 below, visualize an Equation Mat with algebra tiles.  Then answer the questions for each step below. a. What legal move does writing –4 twice represent? b. What legal move does circling the +4 and the –4 represent? c. What does the box around the pic represent? d. Why did Aidan divide both sides by 2? e. Check Aidan’s solution in the original equation.  Is his solution correct?

6-73. The method of recording the steps in the solution of an equation is useful only if you understand what operations are being used and how they relate to the legal moves on your Equation Mat. 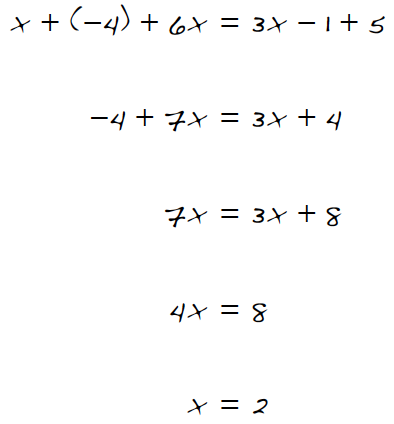pic Find the work shown at right on your resource page for this lesson. a. For each step in the solution, add the missing work below each line that shows what legal moves were used.  You may want to build the equation on an Equation Mat. b. Check that the solution is correct.

6-74. For each equation below, solve for  x.  You may want to build the equation on your Equation Mat.  Record your work in symbols using Aidan’s method from problem 6‑72.  Remember to check your solution. a. −2x + 5 + 2x − 5 = −1 + (−1) + 6x + 2 b. 3(4 + x) = x + 6

6-75. Oliver is building a train depot for his model railroad.  As his final step, he needs to apply rain gutters around the roof of the rectangular building.  He has 52 cm of rain gutters.  The length of the depot is 19 cm.  Explore how Oliver can find the width of the depot by answering the questions below. a. Find the width of the depot using arithmetic (that is, solve the problem without using any variables).  Record your steps. b. Use  w  to represent the width of the depot.  Write an algebraic equation that shows the perimeter is 52 cm, and solve your equation.  Record your steps. c. Which method, the arithmetic or algebraic, did you prefer?  Why?

6-76. For each equation below, solve for  x.  You may want to build the equation on your Equation Mat.  Record your work and check your solution. a. 5x + (−x) − 1 = 11 − 2x b. 3(−x + 2) + x − 1 = −x − 3

6-77. Genny is confused.  She simplified an equation and ended up with the mat shown below.  What is the value of  x? 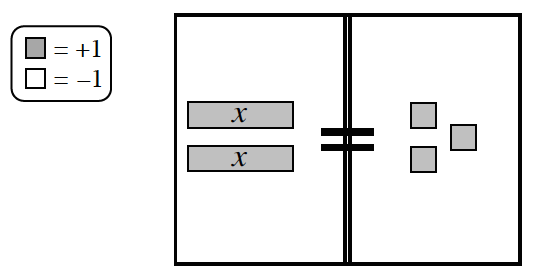pic

6-78. Maggie’s mom agrees to let Maggie buy small gifts for some of her friends.  Each gift costs $4.  Maggie’s mom gave her a budget of $19.  When Maggie went online to order the gifts, she discovered there was a $7 shipping fee no matter how many gifts she bought.

  1. Use arithmetic (without variables) to determine how many gifts Maggie can buy.  Record your steps.
  2. Write an algebraic equation to determine how many gifts Maggie can buy with $19, and solve your equation.  Record your steps.
  3. Compare and contrast the two methods of solving the problem.

6-79. Your teacher will explain the way you will be working on solving the equations below for  x.  You may want to build the equations on your Equation Mat.  Record your work and check your solution.

  1. 2(x + 1) + 3 = 3(x − 1)
  2. −2x − 2 = 3(−x + 2)
  3. 3 + 4(2 − x) = 3x + (−x) − 7
  4. 6(3 − x) + (−20) = 10 + 3(4x + 2)

6-80. LEARNING LOG In your Learning Log, explain what it means to solve an equation.  What is a solution?  Be sure to give an example.  Title this entry “Solving Equations and Checking Solutions” and include today’s date. Assignment: 6.2.3 Extra Practice Problems [/expand]

[expand title=”How can I model it?”] Engineers investigate practical problems to improve people’s quality of life.  To investigate solutions to problems, they often build models.  These models can take various forms.  For example, a structural engineer designing a bridge might build a small replica of the bridge.  Civil engineers studying the traffic patterns in a city might create equations that model traffic flows into and out of a city at different times. In this lesson, you will be building equations to model and solve problems based on known information.  As you work today, keep the following questions in mind.

What does  x  represent in the equation?
How does the equation show the same information as the problem?
Have I answered the question?

6-103. Today your team will be responsible for solving a problem and sharing your solution with the class on a poster.  It is important that your poster communicates your thinking and reasoning so that people who look at your poster understand how you solved the problem.  Your poster should include: Connections between the words in the problem and the relationships in your table and/or equation.  Connections can be made with arrows, colors, symbols, and/or labels.

  • Variables that are defined completely.
  • An equation to represent the problem.
  • Your solution to the problem.
  • The answer declared in a sentence.
  • An estimation verifying that the total of your solutions is reasonable.

Begin by solving one of the problems below and writing an equation.  Make sure to define the variable you use and answer the question(s) being asked.  Using the 5-D Process, including numerical trials, may be helpful.

  1. Hong Kong’s tallest building, Two International Finance Center, is 88 stories tall.  The former Sears Tower in Chicago is eight stories taller than the Empire State Building in New York City.  If all of the buildings were stacked on top of each other, the combined heights would have 300 stories.  How many stories does the Sears Tower have?
  2. Have you ever driven or walked across a suspension bridge?  There are many suspension bridges in the world of different lengths that allow people to travel across rivers, bays, and lakes.The Mackinac Bridge in Michigan is 1158 meters long.  The Tsing Ma Bridge in Hong Kong is 97 meters longer than the Golden Gate Bridge in California.  Together, all three bridges have a length of 3815 meters.  How long is the Tsing Ma Bridge?
  3. Elevations found in the United States range from California’s Death Valley at 282 feet below sea level to Alaska’s Mount McKinley, also known as Denali, at 20,320 feet above sea level.The highest elevation in Delaware is 106 feet higher than the highest elevation in Florida.  Louisiana’s highest elevation is 190 feet higher than Florida’s highest elevation.  If you climbed from sea level to the highest points in Delaware, Florida, and Louisiana, you would only climb 1331 feet.  How high is the highest elevation in each of the three states?
  4. Most states in the United States are divided into counties.  Some counties are very large, while some are very small.  Different states have different numbers of counties.  Pennsylvania has five less than twice as many counties as Oregon.  Florida has one less county than Pennsylvania.  Together, the three states have 169 counties.  How many counties does each of these three states have?
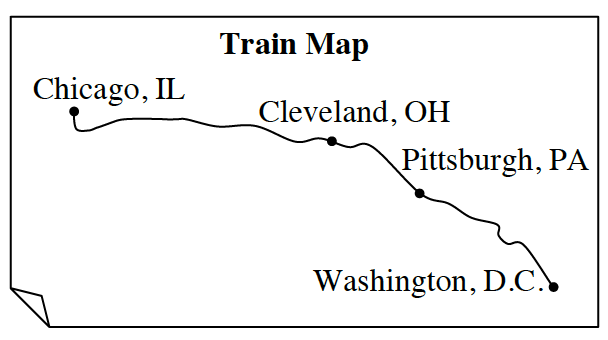  5. picA train from Washington, D.C. to Chicago stops first in Pittsburgh and then in Cleveland.  The distance from Washington, D.C. to Pittsburgh is 30 miles less than twice the distance from Pittsburgh to Cleveland.  The distance from Cleveland to Chicago is 220 miles more than the distance between Pittsburgh and Cleveland.  If the entire train ride is 710 miles, how far is the train ride from Cleveland to Chicago?

6.2.5 Solving Word Problems [/expand]

[expand title=”Is there always a solution?”] Are all equations solvable?  Are all solutions a single number?  Think about this: Annika was born first, and her brother William was born 4 years later.  How old will William be when Annika is twice his age?  How old will William be when Annika is exactly the same as his age? In this lesson, you will continue to practice your strategies of combining like terms, removing zeros, and balancing to simplify and compare two expressions.  You will also encounter unusual situations where the solution may be unexpected.  As you work today, focus with your team on these questions:

What if both sides are not equal?
Are there many values of  x  that will make the expressions equal?
Is there always a solution?

 

6-116. Many students believe that every equation has only one solution.  However, in the introduction to this lesson you might have noticed that if Annika was four years older than her brother, William, they could never be the same age.  Some situations have one solution, others have no solution, and still others have all numbers as solutions. For each of the following equations, reason with your team to decide if there is “One solution,” “No solution,” or “All numbers are solutions.”  If there is a single number solution, write it down.  If you are not sure how many solutions there are, have each member of your team try a number to see if you can find a value that makes the equation work.

  1. x = x
  2. x + 1 = x
  3. x = 2x
  4. x + x = 2 + x
  5. x + x = x − x
  6. x + x = 2x
  7. x · x = x2
  8. x − 1 = x

6-118. SPECIAL CASES, Part One Use the equation  8 + x + (−5) = (−4) + x + 7 to complete parts (a) through (c). a. Build the equation on your Equation Mat using algebra tiles and simplify it as much as possible.  Record your steps and what you see when you have simplified the equation fully.  Draw a picture of your final mat. b. Have each member of your team test a different value for  x  in the original equation, such as   x = 0, x = 1, x = −5, x = 10, etc.  What happens in each case? c. Are there any solutions to this equation?  If so, how many?

6-119. SPECIAL CASES, Part Two Use the equation  x + x + 2 = 2x to complete parts (a) through (c). a. Build the equation on your Equation Mat using algebra tiles and simplify it as much as possible.  Record your steps and what you see when you have simplified the equation fully.  Draw a picture of your final mat. b. Have each member of your team test a different value for  x  in the equation, such as  x = 0, x = 1, x = −5, x = 10, etc.  What happens?  Is there a pattern to the results you get from the equation? c. Did you find any values for  x  that satisfied the equation in part (a)?  When there is an imbalance of units left on the mat (such as 2 = 0), what does this mean?  Is x = 0 a solution to the equation?

6-120. Keeping these special cases in mind, continue to develop your equation-solving strategies by visualizing and solving each equation below.  Remember to build each equation on your mat, if needed, to simplify as much as possible, and to solve for  x.  Identify if one number is the solution, if any number is the solution, or if there is no solution.  Record your steps.

  1. −x + 2 = 4
  2. −3 + x = 2(x + 3)
  3. 5x + 3 + (−x) = 2x + 1 + 2x + 3
  4. 3x + 7 + (−x) + −2 = 2x + 5
  5. 4 + −3x = 2
  6. 3x + 3 = 4 + x + (−1)

6-121. Additional Challenge: For each of the parts below, create your own equation (involving at least three steps) that has the given solution.

  1. x = –2
  2. x = 
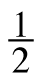
  3. no solution
  4. all numbers

Assignment: 6.2.6 Homework [/expand]