[expand title=”Introduction”]
Dan Meyer – Dueling Discounts (Three Acts)
[/expand]
[expand title=”How can I make it smaller or bigger?”]
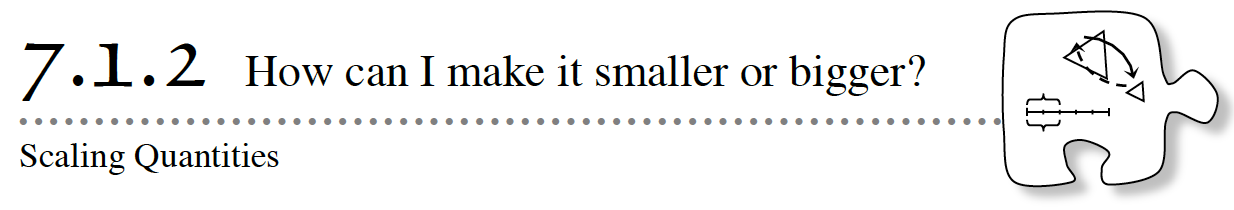
In Chapter 5, you learned how to find the percent of a number by making a diagram to relate the part to the whole and find the desired portion. This calculation is fairly straightforward if the percent is a multiple of 10, like 40%, or can be thought of as a fraction, like 
= 25%. However, it can be more challenging if the percent is something like 6.3% or 84.5%.
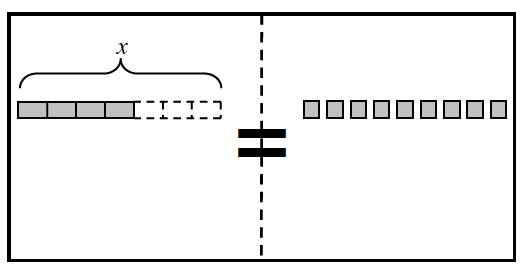
7-16. Dana is training for a bicycle race. He can ride his bike 25 miles per hour.
One day, when he had been riding for 
of an hour, he had to stop and fix a flat tire. How many miles had he ridden when he stopped? The diagram below may be useful.
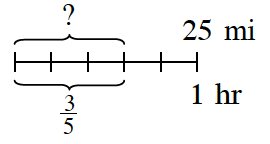
7-17. Matt thought about problem 7-16 and drew the diagram at right. Look at Matt’s drawing and decide how he is thinking about this problem.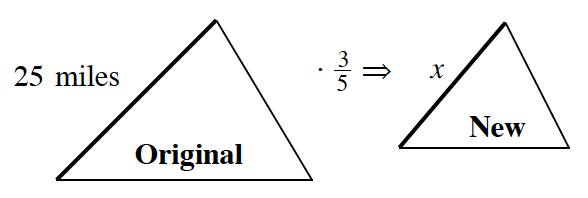
a. Write an equation that uses the scale factor to find x.
b. What connection is Matt making between finding a distance using the rate and time (as you did in problem 7-16) and using a scale factor with similar figures? How are the situations alike and how are they different?
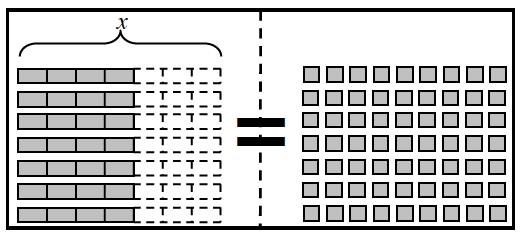
7-18. In the two previous problems, is used in two ways: first, as time in the rate problem 
·hrs, and second, as the scale factor in the similar triangle problem used to find three fifths of 25 miles. Both of these situations resulted in an equivalent calculation: 25 ·= 15. How else could this be written?
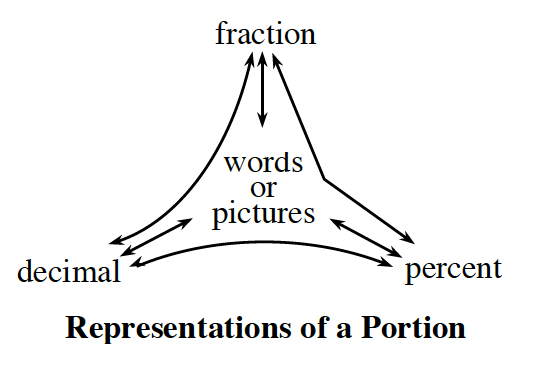a. Using the portions web shown at right, work with your team to find two other ways to write the equation 25 ·= 15. For example, one way might be 25 ·
= 15.
b. If you did not already find it, what percent would be equivalent to ? Use this percent to write a statement in words and symbols that is equivalent to 25 ·= 15.
c. Use the idea of scaling to find the following values. Write an expression using either a fraction or a decimal, and then find the result.
- 90% of 25 miles
- 8% of $75
- 25% of 144
7-19. Josea went out to dinner at an Indian restaurant. The total bill was $38. She wanted to leave a 15% tip.
a. If you use the idea of scaling to find the tip amount, what would she need to multiply by? As you talk about this with your team, consider:
- How could you represent this multiplier as a fraction?
- How could you represent it as a decimal?
- Does it make a difference which representation, fraction or decimal, you use to solve this problem?
- Which do you think will be easier?
b. How much should Josea leave for the tip? Show your calculations.
c. If Josea changes her mind and wants to leave a 20% tip instead, how much will this be?
7-20. While shopping for a computer game, Isaiah found one that was on sale for 35% off. He was wondering if he could use 
as a multiplier to scale down the price to find out how much he would have to pay for the game.
a. If Isaiah uses as a scale factor (multiplier), will he find the price that he will pay for the game? Why or why not?
b. There is scale factor (multiplier) other than 35% that can be used to find the sale price. What is it? Draw a diagram to show how this scale factor is related to 35%. Label the parts of your diagram “discount” and “sale price” along with the relevant percents.
c. How much will Isaiah have to pay for the game if the original price is $40? Show your strategy.
Assignment: 7.1.2 Homework
[/expand]
[expand title=”Which multiplier should I use?”]
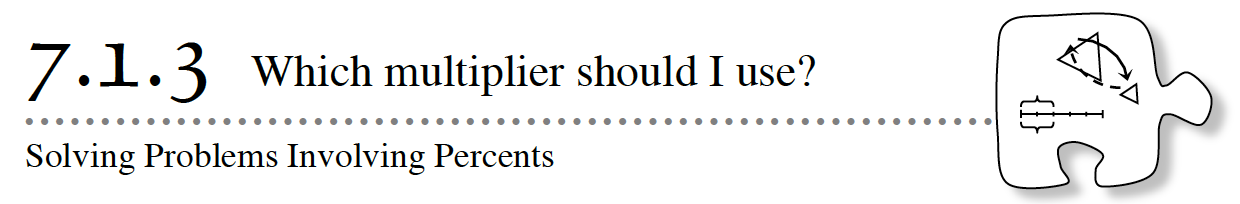
As you have seen many times in this course, there is usually more than one way to solve a problem. When a problem uses portions (fractions, decimals, or percents), there are different ways to write the numbers and different solving strategies to choose from. Today you will look at the different multipliers that can scale a quantity and see what each of them will help you find. As you work with your team today, consider the questions below.
7-27. Hugo and his family were shopping and purchased a new bed. The bed was a great deal at 60% off of the original cost. The bed originally cost $245.
a. Draw a diagram for this situation.
b. If Hugo scales (multiplies) the original price of the bed by 60%, what will his result represent?
c. What should Hugo scale (multiply) the original price by to find the new price of the bed?
d. Work with your team to find the sale price of the bed in two different ways, that is, using two different multipliers (scale factors). How do your answers from your two methods compare?
7-28. Hugo’s older sister, Sandra, had the same summer job for the past two years. Last year, she worked the entire summer and was paid a salary of $3,000. This summer, she is going to get a 6% raise in pay. To figure out how much she will make, Sandra drew the following diagram.
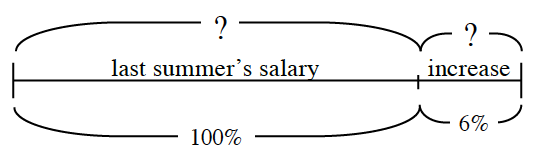a. Copy the diagram on your paper and fill in the missing information.
b. Since Sandra’s salary is increasing, does it make sense that her scale factor (multiplier) should be less than 1, equal to 1, or more than 1? Why?
c. The diagram shows Sandra’s original salary and the amount of the increase. What is the scale factor (multiplier) between her original salary and her new salary? That is, what number could Sandra multiply the original salary by to get the new salary?
d. Show two ways that use different scale factors (multipliers) that Sandra can use to compute her new salary.
7-29. Miranna teaches gymnastics lessons at summer camp. She is paid $12.50 per hour.
a. If Miranna were offered a raise of 100% per hour, what would her new hourly rate be? What percent of her original pay would she be paid?
b. Miranna is offered a raise of 75% of her hourly rate to teach a private lesson. How much per hour would she be paid for the private lesson?
What percent of her original pay would she get?
c. What is the relationship between the percent raise that Miranna gets and her new pay as a percent of her original pay? How is this related to the scale factor (multiplier) between her original pay and her new pay?
7-30. Liam was working on a problem and drew a diagram like the one below. He then wrote the equation ($72)(0.14) = x. Does his equation agree with his diagram?
a. If you agree, then solve his equation for x.
b. If you disagree, write and solve a new equation that will find x in his diagram.
7-31. Additional Challenge: Ramon went to the corner store and bought more notebook paper to do his homework. The cost for the paper was $7.50, but he also had to pay the 8.1% sales tax. How much will the notebook paper cost Ramon? If Ramon gives the clerk $10, how much change should he receive?
7-32. LEARNING LOG
In your Learning Log, describe how you scale a quantity. For example, how do you know what multiplier (scale factor) to use? How can you tell if your multiplier should be more than one? Title your entry “Scaling Quantities” and include today’s date.
Assignment: 7.1.3 Homework
[/expand]
[expand title=”How can I solve it?”]
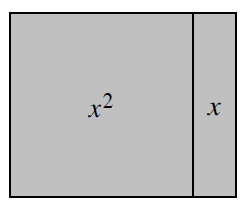Throughout this course, you have worked with quantities represented in multiple ways. You have seen that 
, 0.75, 75%, and 
each represent the same portion even though they look different. In your work with algebra tiles, you visualized and described perimeters in different ways. For example, the perimeter of the algebra tiles at right can be described by the expressions 3x + 2 + x, x + 1 + x + 1 + x + x, or 4x + 2x + 2 − 2x units.
In this lesson, you will develop strategies to solve a new type of equation: equations with coefficients that are fractions. Recall that coefficients are the numerical part of a term, such as the 5 in 5x and the 
in x2. You will choose between different strategies based on how the problem is represented, what diagram you draw, or whether you represent the situation with an equation. As you explore solving strategies today, keep these questions in mind:
How can I represent it?
7-39. ARE WE THERE YET?
The Sutton family took a trip to see the mountains in Rocky Mountain National Park. Linda and her brother, Lee, kept asking, “Are we there yet?” At one point, their mother answered, “No, but what I can tell you is that we have driven 100 miles and we are about 
of the way there.”
Linda turned to Lee and asked, “How long is this trip, anyway?” They each started thinking about whether they could determine the length of the trip from the information they were given.
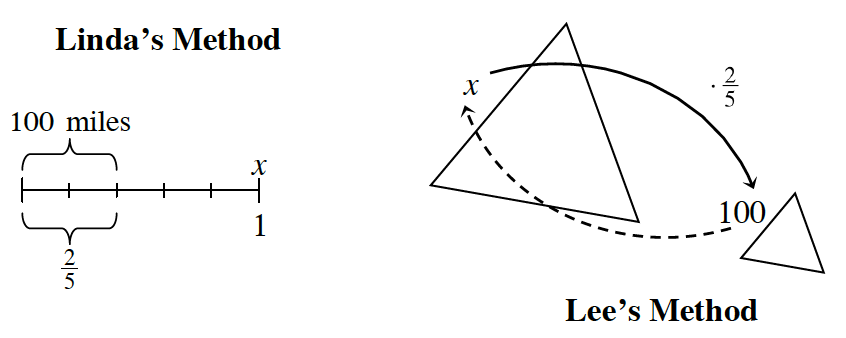
a. Explain how both Linda’s work and Lee’s work illustrate the situation described by their mother. What does x represent in each diagram?
b. What equation could represent this situation? Use the scale factor (multiplier) to represent this situation in an equation. Let x represent the total distance in miles.
c. Is the answer going to be more or less than 100 miles? Explain your thinking.
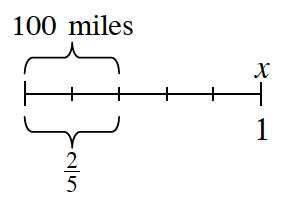
7-40. Linda remarked to Lee, “When I look at my diagram, I see that the total distance is two-and-a-half times the distance we’ve driven.”
a. Do you agree? How can you add labels to Linda’s diagram to show 2
times the distance?
b. How long is the trip? Show how you know.
7-41. Lee thinks what he knows about similar triangles can help.
a. Review problem 7-22, which involved similar triangles. How are the scale factors related?
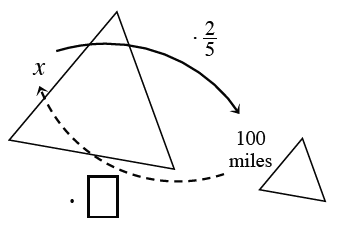b. How can the relationship of the scale factors between similar shapes help Lee? Find the missing scale factor in his diagram at right. That is, what could he multiply 100 by to solve for x?
c. Use the new scale factor to find x. Does your answer agree with the one you found in part (b) of problem 7-40?
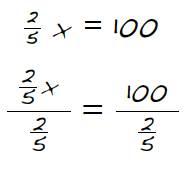
7-42. As Linda and Lee were talking about the problem (from problem 7-39), their mother overheard and offered them another strategy: “Here is how I would start solving the problem.” She showed them the work at right.
a. “I see a Giant One!”exclaimed Lee. Where is the Giant One? Help rewrite the left side of the equation.
b. One way of making sense of 
is as 100 ÷ = ?.
This could be read, “How many two-fifths are in one hundred wholes?” With your team, find one way to explain how you could figure out how many two-fifths are in 100.
7-43. Lee began to wonder how his diagram could help him solve his mother’s equation (from problem 7-42). He showed his work below.
a. How does Lee’s work relate to the similar-triangles diagram? What is equal to?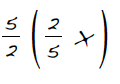 
b. Finish Lee’s work to solve for x. Then check your solution.
7-44. Linda and Lee wondered how these new equation-solving strategies would work with different equations. They made up more equations to try to solve. Copy the equations below on your paper and solve each equation using one of the strategies from this lesson. How did you decide which strategy to use?
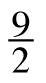x = 27- 12 =
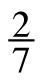x - −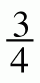x = 21
Assignment: 7.1.4 Homework
[/expand]
[expand title=”How can I eliminate the fractions?”]
Often, one of the best ways to deal with a challenging task is to find a way to make the task easier. For example, lifting a heavy weight can be made easier with a lever or pulley. Mathematical problems are very similar; often, a challenging problem can be changed to create a new problem that is much easier to solve. In this lesson, you will develop strategies for rewriting a complicated equation into an equivalent equation that is more familiar and easier to solve.
7-51. COMMUNITY SERVICE
The community service club at North Middle School is planning to paint apartments at the local senior citizen center next week. The club needs your help to determine how many apartments they should be able to paint in a day. Earlier in the year, when only 
of the students worked, they painted 9 apartments in one day. Next week, all of the students are available.
- Assume that all of the student workers contribute equally to the work. If x represents the number of apartments that can be painted by all of the students in the club, use a multiplier and your understanding of scaling to represent this situation as an equation.
- Choose a strategy to solve your equation in part (a). What does your answer represent? Be ready to share your strategy.
7-52. HOW CAN I MAKE WHOLES?
Janice, the club’s president, began to think about how she could visualize x to help her solve her equation (from problem 7-51). She recalled using algebra tiles to represent x. In her mind, she visualized the diagram at right.
- Does this Equation Mat represent your equation from problem 7-51? Why or why not?
Janice recognized that these numbers were not easy to work with, since she did not have whole tiles. After working on her paper for a while, she said,“Maybe I can make whole tiles using more than one set of partial tiles.” She drew the diagram shown at right.What is her new equation as represented in this picture?- With your team or class, discuss Janice’s strategy for solving this equation. During your discussion, answer the following questions (in any order):
- What made Janice’s strategy different than what you did in Lesson 7.1.4?
- How many sets of 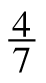x did Janice use to get a whole number of algebra tiles?
- Why did the right-hand side of the equation change?
- How does the number of sets Janice used relate to the equation you wrote in part (a)?
7-53. Will the strategy of turning fractions into integers from problem 7-52 work with other equations, such as x = 8? Consider this question as you answer the questions below.
- How many sets of 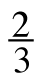x would make a whole number of x‑tiles?
- Solve for x using Janice’s method from problem 7-52. How could you record your work on your paper?
- Show how your solution is also the number of two thirds in 8 wholes (written 8 ÷ ).
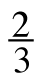7-54. Janice wondered if the method of creating whole-number x‑terms would work with decimals. Suppose an item was marked 15% off and the sale cost was $36.21. She wrote the equation below:
- Why did she write 0.85 in her equation?
- Is there a number she can multiply both sides of the equation by to get an integer coefficient (so there is no decimal)? If so, list at least one. If not, explain why not.
- Use Janice’s strategy to solve the equation. What was the original price of the item?
- Does this method work for all equations with decimal coefficients? What if you wanted to solve the equation 1.2x = 14? What about 0.999x = 71.2? Discuss these equations with your team and write down your conclusion.
7-55. Solve each equation below by changing the number that x is being multiplied by (the coefficient of x) to an integer. Check your answer.
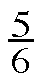x = 4- 0.8x = 19
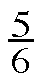- x = 12
- 0.12x = 1
7-56. LEARNING LOG
In your Learning Log, summarize at least two strategies to solve an equation with fractional (or decimal) coefficients. Provide an example for each strategy and include a diagram. Title this entry “Solving Equations with Fractional Coefficients” and include today’s date.
Assignment:
[/expand]
[expand title=”How can I solve complicated equations?”]
In this lesson, you will continue to develop strategies to rewrite a complicated equation into an equivalent equation that is more familiar and easier to solve.
7-63. Chari volunteers over the summer in a veterinarian’s clinic. The doctor has told Chari to determine the correct dose of medicine to give to the cat, Sweetie, who weighs 9.5 pounds. The dosage (in ml) for a 9.5-pound cat is given by x in the formula below.
+
=
Chari had never solved such a complicated equation before.
7-64. Examine the equation below.
−= 7
- Multiply each term by 4. What happened? Do any fractions remain?
- If you have not already done so, decide how you can change your result from part (a) so that no fractions remain. Then solve the resulting equation.
- Multiplying 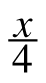−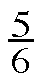= 7 by 4 did not eliminate all the fractions. What could you have multiplied by to get rid of all the fractions? Explain how you got your answer and write the equivalent equation that has no fractions.
- Solve the resulting equation from part (c) and check your solution in the original equation.
7-65. The method you used in problem 7-64 to eliminate fractions from an equation can be called Fraction Busters, because the multiplication of the equation by a common denominator or several of the denominators eliminates, or “busts,” the fractions. The result is an equation with no fractions.
Chari is attempting to solve the equation below.
−
=
a. What is a common denominator for these fractions? Discuss with your team how you could use the common denominator to eliminate the fractions in Chari’s equation.
b. If you have not already done so, find an equivalent equation without fractions.
c. Solve for b and check your answer.
7-66. Chari is worried that Sweetie is too thin. The doctor tells Chari that the weight of a typical cat like Sweetie is given by w in the formula below. A healthy cat is within 2 pounds of the typical weight. Is Sweetie too thin?
= 5.5
7-67. Work with your team to solve the following equations. Can you find a number to multiply by that will eliminate all of the fractions in one step?
+
=
=
+
−=
+ 
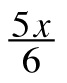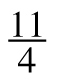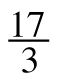
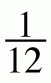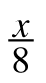
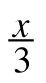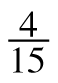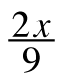
7-68. Use Fraction Busters in reverse to rewrite the equations below with smaller integer coefficients to make them easier to solve. Solve each equation and check your solution.
- 300x − 1500 = 2400
- 36 − 3r = 18 − 6r
7-69. Rewrite the equations below to make them easier to solve. Solve each equation and check your solution.
- 0.04x + 0.16 = 0.06 + 0.08x
- 4r2 + 48 = 4r + 24 + 4r2 − 8r
+ 
=
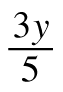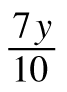+ 15
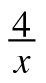+11=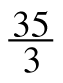
Assignment: 7.1.6 Homework
[/expand]
[expand title=”Percent of what?”]
Perhaps you have heard an adult say something like, “When I was growing up, it only cost a dime to go to the movies!” The rate at which prices increase over a period of time, called inflation, is one of the many things that mathematics can help you understand. In this lesson, you will be using diagrams and computations to calculate the way quantities (like cost or height) change.
As you work today, keep the following questions in mind:
7-76. WHAT IS THE PERCENT INCREASE?
Several years ago, Joe started a lawn-care business. Due to rising costs, he needs to increase his prices. He is concerned, however, because he has heard that if he raises his rates more than 33%, he might lose business. At right is a letter he sent to his clients.
Joe began to wonder about how the increase in his fees could be expressed in terms of a percent.
a. Joe wants to determine the scale factor (multiplier) for the price increase and wrote the following equation:
12.50x = 15
Explain how this expression represents this situation. What does x represent?
b. Solve the equation above to determine the scale factor for his change in fees. Represent this multiplier (scale factor) as a fraction, as a decimal, and as a percent.
c. How could this situation be represented with a line diagram? With your team, copy and complete the diagram below. Then answer and do the following: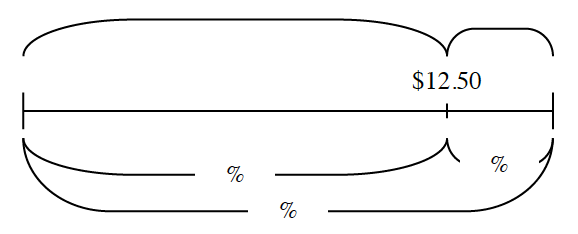
- Which portion of the diagram corresponds to the original price? Circle and label this part “original.”
- Which portion of the diagram corresponds to the change in price? Circle and label this part “change.”
d. When Joe raised his rates, what was the percent increase? That is another way of asking: What percent of the original price did the price change? Should Joe expect to lose business?
7-77. Paige needs your help! She wants to convince her grandmother to let her sign up for a rock-climbing class. The class normally costs $50, but the school is offering a special price of $34. Paige’s grandmother wants to know what percent of the cost of the class she would save.
a. Without calculating, estimate the percent of the discount.
b. With your team, determine the percent change in the price of the class. Use the prompts below to help guide your team’s discussion.
- Draw a diagram or write an equation that represents the situation.
- What is the original (whole) value? Indicate this on your diagram or in your equation.
- What percent is the change? Find and indicate this on your diagram or in your equation.
- Does this situation represent an increase or decrease?
7-78. The percent change is a comparison of the amount of change to the original amount. If a number increases from the original amount, it is called percent increase. If the number decreases from the original, it is called a percent decrease.
a. What is the percent change from $30 to $33? Is this a percent increase or decrease? To answer this question:
- Draw a diagram to represent the problem.
- Determine if it is a percent increase or decrease.
- Calculate the percent change.
b. What is the percent change from $33 to $30? Is this a percent increase or decrease? To answer this question:
- Draw a diagram to represent the problem.
- Determine if it is a percent increase or decrease.
- Calculate the percent change.
c. If both parts (a) and (b) above have a change of $3, why are the percent changes different? Explain.
7-79. To attract new customers, a shoe company called Shoe Fits will raise its prices 10% and then offer a 10%-off coupon.
a. Without doing any calculations, consider the following question: If a coupon is used, do you think the final price will be more than, less than, or the same as the original price? Discuss this with your team and be ready to share your thinking with the class.
b. Akari wants to use a coupon to buy a pair of shoes that originally cost $46. What will the increased price be? What will be the price after the 10%-off coupon is used? Show all calculations. Does this result confirm your answer to part (a)?
c. Akari had assumed that if the price increased 10% and then he received a 10% discount, it would return to the original price. Explain why this did not happen.
Assignment: 7.1.7 Homework
[/expand]
[expand title=”How does it change over time?”]
When banks lend money, they charge interest, which is a fee for letting the borrower use the money. Interest is usually expressed as a percent of the amount borrowed and is added to the amount that the borrower owes. For example, a bank might charge someone an 8% annual (yearly) interest rate for borrowing $500. In addition, if you have money in a savings account, banks generally pay interest to you on the money in the account. So by leaving your money in a bank, you can earn more money.
There are different ways of calculating interest, and each one creates different patterns of growth. As you work with your team to investigate one kind of interest called simple interest, ask these questions to focus your discussion:
What patterns do you see?
How can you show the connection?
7-86. RENTING THE HALL
The student council is planning a spring celebration. Unfortunately, to rent a hall for the event, they will need to pay a deposit in advance of the event. Since they have not started selling tickets yet, they asked the Parent-Teacher Association for a loan of $825 for the hall rental. The PTA agreed, but said it would charge 2% simple interest each week until the loan is paid back.
Ms. Becker, the student-council advisor, explained to the students that the amount of the loan ($825) is called the principal amount. Until the loan is paid back, 2% (called the weekly interest rate) of the principal amount will be added each week to the amount owed.
a. How much money in interest will the PTA charge each week?
b. If the student council borrows $825, how much will it owe after 1 week? After 3 weeks? Show your calculations.
c. How much would the student council owe two months (8 weeks) from now? Be prepared to justify your strategy.
7-87. The student-council members realized that they would also need funds before the event to pay the DJ and photographer a deposit. They will need a second loan of $1000 to pay for these two expenses.
a. If the PTA also charges them 2% weekly simple interest for this loan, how much will be added to this loan each week?
b. The PTA has decided that to cover its costs, it only needs to earn $18 interest each week. What percent weekly interest should the PTA charge the student council for this loan? Be prepared to share your strategy.
7-88. A loan agreement between the student council and the PTA has finally been reached, but the PTA will not loan the full $1825 requested. To make sure everyone understands the agreement, the PTA created the table below.
| Number of Weeks | Calculations | Total Loan Amount |
| 0 | $1250 | $1250 |
| 1 | $1250 + $18.75 | $1268.75 |
| 2 | $1250 + $18.75 + $18.75 | $1287.50 |
| 3 | ||
| 4 |
a. Based on this table, how much will the student council borrow? What is the percent interest?
b. How much will the student council owe after 3 weeks? After 4 weeks? Show your calculations.
c. How is the amount of money that the student council owes changing each week? Show how this change can be found in your table.
d. The student-council president wants to be able to check quickly how much the student council owes at any point. Use your table to write a variable expression that shows the amount of money the club owes the PTA after any number of weeks. Make sure to define your variable.
e. The president figured out that if the student council does not pay off the loan by the end of the school year, it would owe $1500. How many weeks of school are left? Use your expression from part (d) to write and solve an equation to answer this question.
7-89. SHOPPING AROUND
The treasurer of the student council decided to look into other funding options for the DJ and the photographer. With your team, examine how each loan would grow and find a way to compare the loans. Assume that a month is 4 weeks. Then find answers to the questions below.
b. What is the monthly interest rate the Booster Club is offering? Show how you got your answer.
c. For which loan would the student council owe the most money overall after 3 months? Justify your answer.
Assignment:
[/expand]
[expand title=”What is the missing number?”]
Throughout this course, you have made connections between different representations of proportional relationships. In this lesson, all of these ideas will come together to uncover a new strategy for finding missing quantities in proportional relationships.
7-96. In Chapter 4, Kaci was trying to figure out how many pounds of Havarti cheese she could buy for $10, knowing that 3 pounds costs $7.50. She wrote the equivalent ratios below.
Work with your team to brainstorm a list of all of the methods that you can think of that Kaci could use to find the information she is missing. Be prepared to share your ideas with the rest of the class.
7-97. Graeme knows that he earns $4.23 every half hour. He wanted to know how much money he would earn after one full week of work (40 hours). He wrote the equivalent ratios below and quickly sees a way to find his answer.
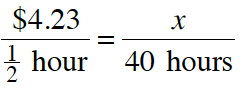
b. Solve Graeme’s equation.
c. Graeme wants to know how long it will take him to earn $1000. Write and solve an equation to help him figure it out.
7-98. Shiloh knows that it takes 5 cups of flour to make 2 recipes of cookies. He has 13 cups of flour left in his cupboard. He wants to know how many recipes he can make. He wrote the equivalent ratios below.
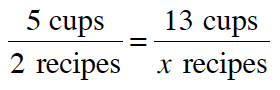
“If it takes 5 cups of flour to make 2 recipes, then it takes 2 cups of flour for each recipe. This is the multiplier. Can’t you just use the multiplier to write an equation?”
Carolyn then wrote the equation F = 2 R where F stands for cups of flour and R stands for the number of recipes. As Carolyn wrote the equation below, she said, “Then I would solve this equation to find out the number of recipes.”
13 = 2 R
a. Compare Shiloh and Carolyn’s equations. Are they correct? Why or why not?
b. Which equation is easiest to solve? Solve it.
c. Does your solution work in both Shiloh and Carolyn’s equations?
7-99. Find the missing information in each set of equivalent ratios below, using any method. Be sure that you record your process so that others can see what you did.
=
=
=
=
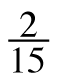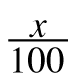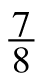
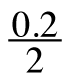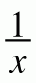
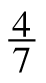
Assignment: 7.2.1 Homework
[/expand]
[expand title=”How can I find the missing value?”]
You have examined several proportional situations (such as the price of yogurt versus the number of pounds of yogurt) and non-proportional situations (such as the value of a college fund over time). Today you will continue to develop strategies for solving proportional equations.
7-106. J.R. reduced figure A at right to create similar figure B.
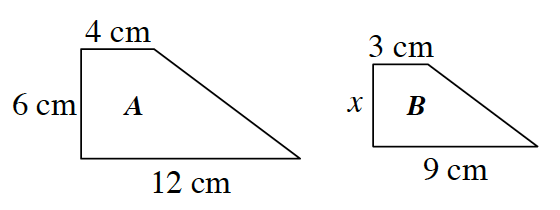
a. Write all of the ratios that compare the corresponding sides of figure B to figure A. What is the relationship between these ratios? How do you know?
b. One of the relationships between the sides can be written as =. Find two different ways to find the value of x in this equation. Is your answer reasonable? Be ready to share your strategies with the class.
7-108. Solve the problems below.
a. Use Leticia’s method of undoing division to solve this proportion: 
=
. When you find p, replace the value in the original proportion to confirm that the two ratios are equal.
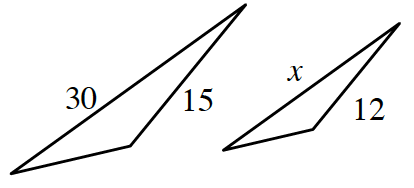
b. Write and solve a proportional equation for x for the similar triangles at right. Then use Avner’s method of undoing both denominators (Fraction Busters) to solve for x.
c. An apple-juice container has a tiny hole in it, so it is slowly leaking. If the container leaks three ounces every 19 minutes, how long will it take for the 16 ounces of juice in the container to leak out? Write a proportional equation and solve.
7-109. For each problem below, decide if the situation is proportional. If the problem is proportional, say so, and then solve the problem using any strategy you choose. If the problem is not proportional, explain why not, and then solve the problem.
a. Steve drove 130 miles from Portland to Tacoma in 2 hours. If he continues to drive at the same speed, how long will it take him to drive 390 miles?
b. At an amusement park, you pay a $15 entrance fee and then $4 for each ride you go on. How much will it cost you to go on seven rides?
c. Armando has collected 39 bottle caps in the past three months. At this rate, how many bottle caps will he have in five months?
d. The grocery store sells 3 limes for 99 cents. At this rate, how much will a dozen limes cost?
e. Margarit drove her friends to a movie. She drove for 30 minutes at 10 miles per hour in heavy traffic, and then she drove for 15 minutes at 40 miles per hour. How far did she travel in those 45 minutes?
7-110. After Ramona had solved several proportional equations, she noticed a pattern. “When we eliminated both of the fractions by multiplying by both denominators, we ended up with something that looks like we just multiplied diagonally.”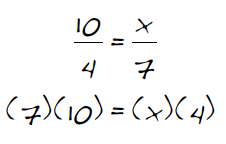
a. What does she mean? For each of the proportions below, apply Ramona’s diagonal multiplying pattern and determine whether the result is a true mathematical equation. Will her pattern always work?
=
=
=
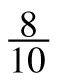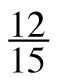
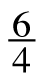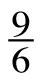
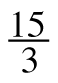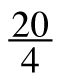
b. Use Ramona’s pattern to solve the equation =
for x.
Assignment:
[/expand]