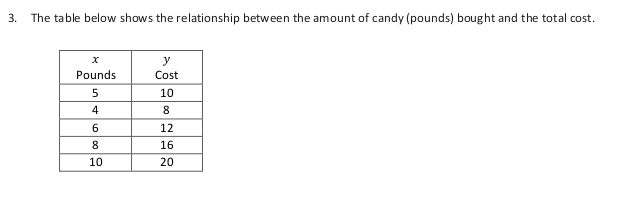Intro Activity
Week 14 – Proportional Relationships
- How do you think Gustavo made his prediction
- Do you agree with Gustavo’s reasoning? Explain why or why not.
4-23. Gustavo decided to look more carefully at his balances for the last few years to see if the bank’s prediction might be a mistake. He put together the table below.

- How has Gustavo’s bank balance been growing?
- Does Gustavo’s money seem to be doubling as the number of years doubles? Explain your reasoning.
- Is the bank’s prediction a mistake? Explain your answer.
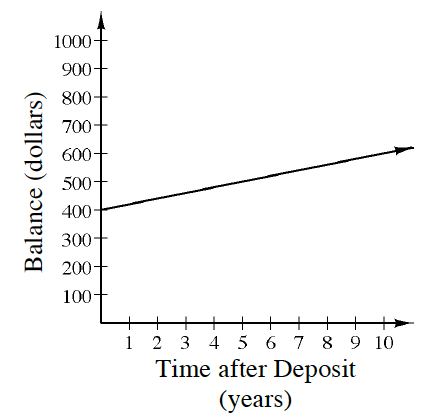
- There is additional information about Gustavo’s account that you can tell from the graph. For example, what was his starting balance? How much does it grow in 5 years?
- Gustavo had assumed his money would double after 10 years. What would the graph look like if that were true? Using a different color, add a line to the graph that represents what Gustavo was thinking.
- Is it possible that Gustavo’s account could have had $0 in it in Year 0? Why or why not?
 With your team:
a. Describe how each graph is the same.
b. Describe what makes each graph different.
c. How do the differences explain why doubling works in one situation and not in the other? Generalize why doubling works in one situation and not in another.
d. The pattern of growth in Sonja’s example of buying birdseed is an example of a proportional relationship. In a proportional relationship, if one quantity is multiplied by a scale factor, the other is scaled by the same amount. Gustavo’s bank account is not proportional, because it grows differently; when the number of years doubled, his balance did not. Work with your team to list other characteristics of proportional relationships, based on Sonja’s and Gustavo’s examples. Be as specific as possible.
With your team:
a. Describe how each graph is the same.
b. Describe what makes each graph different.
c. How do the differences explain why doubling works in one situation and not in the other? Generalize why doubling works in one situation and not in another.
d. The pattern of growth in Sonja’s example of buying birdseed is an example of a proportional relationship. In a proportional relationship, if one quantity is multiplied by a scale factor, the other is scaled by the same amount. Gustavo’s bank account is not proportional, because it grows differently; when the number of years doubled, his balance did not. Work with your team to list other characteristics of proportional relationships, based on Sonja’s and Gustavo’s examples. Be as specific as possible. - What is the relationship between eggs and crepes?
- How many crepes can you make with only one egg?
- How many eggs will be needed for 50 crepes?
- How many crepes can you make with a dozen eggs?
| Eggs | ||||||||
| Crepes |
Week 15 – Unit Rate
- Work with your team to read each new situation below.
- Find the unit rate for each situation.
- Decide whether you think the relationship described is proportional or non-proportional and justify your reasoning.
- Carlos wants to buy some new video games. Each game he buys costs him $36. Is the relationship between the number of games Carlos buys and the total price proportional?
- A single ticket to a concert costs $56, while buying five tickets costs $250. Is the relationship between the number of tickets bought and the total price proportional?
- Vo is four years older than his sister. Is the relationship between Vu and his sister’s age proportional?
- Janna runs at a steady pace of 7 minutes per mile. Is the relationship between the number of miles she ran and the distance she covered proportional?
- Carl just bought a music player and plans to load 50 songs each week. Is the relationship between the number of weeks after Carl bought the music player and the number of songs on his player proportional?
- Anna has a new video game. It takes her five hours of playing the game to master level one. After so much time, Anna understands the game better and it only takes her three hours of playing the game to master level two. Is the number of hours played and the game level proportional?
- Is it reasonable to assume that the weight of the yogurt is proportional to its cost? How can you tell?
- Assuming it is proportional, make a table that lists the price for at least ten different weights of yogurt. Be sure to include at least three weights that are not whole numbers.
- What is the unit rate of the yogurt? (Stores often call this the unit price.) Use the unit rate to write an equation that Jell E. Bean can use to calculate the amount any customer will pay.
- If Jell E. Bean decided to start charging $0.50 for each cup before her customers started filling it with yogurt and toppings, could you use the same equation to find the new prices? Why or why not?
Week 16 – Proportions
- How long would it take her to run 6 miles?
- How far could she run in 15 minutes?
- How fast is she running in miles per hour?
- What is her pace in minutes per mile?
 Assignment:Proportions Worksheet
Assignment:Proportions Worksheet 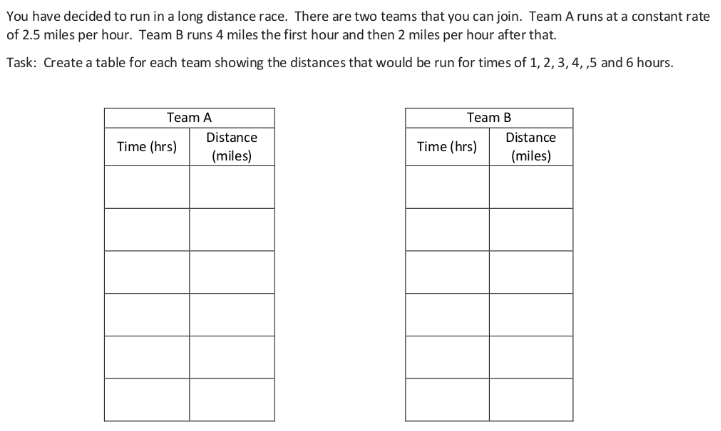
- For which team is distance proportional to time? Explain your reasoning.
- Explain how you know the distance for the other team is not proportional to time.
- If the race were 2.5 miles long, which team would win? Explain.
- If the race were 3.5 miles long, which team would win? Explain.
- If the race were 4.5 miles long, which team would win? Explain.
- For what length of race would it be better to be on Team B than Team A? Explain.
- Using this relationship, if the members on the team ran for 10 hours, how far would each member run on each team?
- Will there always be a winning team, no matter what the length of the course? Why or Why not?
- If the race were 12 miles long, which team should you choose to be on if you wish to win? Why would you choose this team?
- How much sooner would you finish on that team compared to the other team?
- Create a table that shows the time required to build several different quantities of bird houses.
- How many birdhouses can Jackson build in 40 hours?
- Write an equation that can be used to find the time required to build any number of birdhouses.
- How long will it take him to build 35 birdhouses?
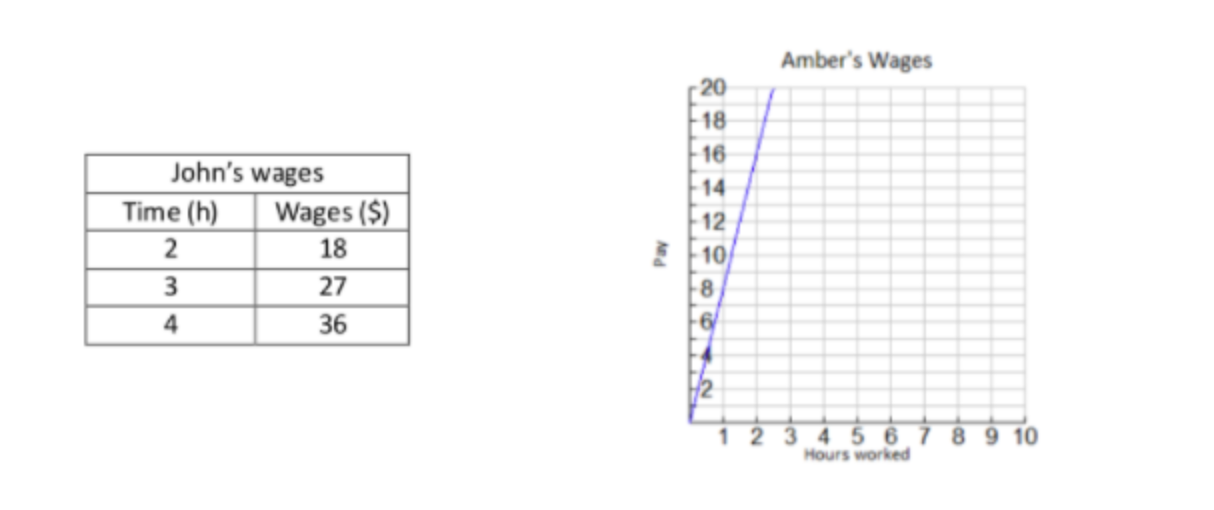
- Determine whether John’s wages are proportional to time. If they are, find the unit rate. If not, Explain why not.
- Determine whether Amber’s wages are proportional to time. If they are, find the unit rate. If not, Explain why not.
- Write an equation to model each person’s wage in relation to hours worked.
- How much would each of them make after working 10 hours?
- How long would it take each worker to make $50?
Additional Resources:
Proportions-Algebraically 8(Mixed)
Proportions-Algebraically 7(Mixed)
Proportions-Algebraically 6(Mixed)
Proportions-Algebraically 5 (Mixed)
4-26. What makes Sonja’s birdseed situation (problem 4-25) different from Gustavo’s college fund situation (problem 4-21)? Why does doubling work for one situation but not in the other? Consider this as you examine the graphs below.

With your team:
a. Describe how each graph is the same.
b. Describe what makes each graph different.
c. How do the differences explain why doubling works in one situation and not in the other? Generalize why doubling works in one situation and not in another.
d. The pattern of growth in Sonja’s example of buying birdseed is an example of a proportional relationship. In a proportional relationship, if one quantity is multiplied by a scale factor, the other is scaled by the same amount. Gustavo’s bank account is not proportional, because it grows differently; when the number of years doubled, his balance did not. Work with your team to list other characteristics of proportional relationships, based on Sonja’s and Gustavo’s examples. Be as specific as possible.
4-27. IS IT PROPORTIONAL?
When you are making a prediction, it is important to be able to recognize whether a relationship is proportional or not.
Your Task: Work with your team to read each new situation below. Decide whether you think the relationship described is proportional or non-proportional and justify your reasoning. Be prepared to share your decisions and justifications with the class.
- Carlos wants to buy some new video games. Each game he buys costs him $36. Is the relationship between the number of games Carlos buys and the total price proportional?
- A single ticket to a concert costs $56, while buying five tickets costs $250. Is the relationship between the number of tickets bought and the total price proportional?
- Vu is four years older than his sister. Is the relationship between Vu and his sister’s age proportional?
- Janna runs at a steady pace of 7 minutes per mile. Is the relationship between the number of miles she ran and the distance she covered proportional?
- Carl just bought a music player and plans to load 50 songs each week. Is the relationship between the number of weeks after Carl bought the music player and the number of songs on his player proportional?
- Anna has a new video game. It takes her five hours of playing the game to master level one. After so much time, Anna understands the game better and it only takes her three hours of playing the game to master level two. Is the number of hours played and the game level proportional?
Assignment: 4.2.1 Homework
 In Lesson 4.2.1, you learned that you could identify proportional relationships by looking for a constant multiplier. In fact, you have already seen a relationship with a constant multiplier in this course. Today you will revisit the earlier situation that contains a proportional relationship.
In Lesson 4.2.1, you learned that you could identify proportional relationships by looking for a constant multiplier. In fact, you have already seen a relationship with a constant multiplier in this course. Today you will revisit the earlier situation that contains a proportional relationship.
Assignment: 4.2.2 Homework

Proportional relationships can be identified in both tables and graphs. Today you will have an opportunity to take a closer look at how graphs and tables for proportional relationships can help you organize your work to find any missing value quickly and easily.
4-46. Robert’s new hybrid car has a gas tank that holds 12 gallons of gas. When the tank is full, he can drive 420 miles. Assume that his car uses gas at a steady rate.
- Is the relationship between the number of gallons of gas used and the number of miles that can be driven proportional? For example, does it change like Sonja’s birdseed prediction, or is it more like Gustavo’s college savings? Explain how you know.
- Show how much gas Robert’s car will use at various distances by copying and completing the table below.
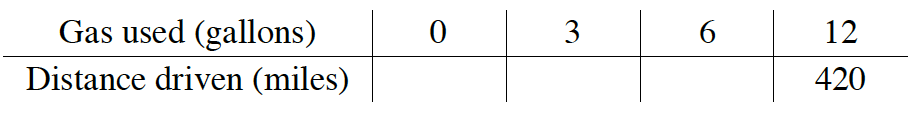
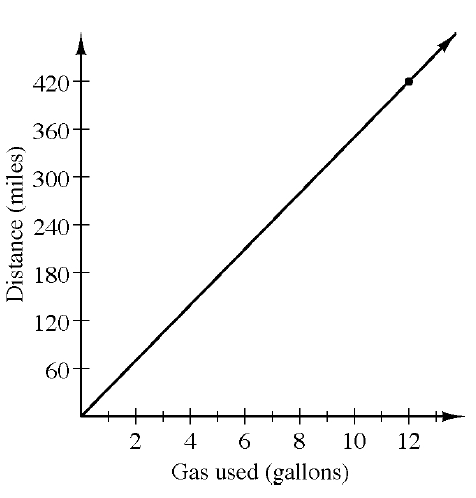 Robert decided to graph the situation, as shown below. The distance Robert can travel using one gallon of gas is called the unit rate. Use Robert’s graph to predict how far he can drive using one gallon of gas. That is, find his unit rate.
Robert decided to graph the situation, as shown below. The distance Robert can travel using one gallon of gas is called the unit rate. Use Robert’s graph to predict how far he can drive using one gallon of gas. That is, find his unit rate.- While a graph is a useful tool for estimating, it is often difficult to find an exact answer on a graph. What is significant about the point labeled (1, y)? How can you calculate y?
- Use the table in part (b) and your result in part (d) to find Robert’s unit rate.
- Work with your team to write the equation to find the exact number of miles Robert can drive with any number of gallons of gas. Be prepared to share your strategy.
- Use your equation to find out how many gallons of gas Robert will need to drive 287 miles. .
4-47. THE YOGURT SHOP
Jell E. Bean owns the local frozen yogurt shop. At her store, customers serve themselves a bowl of frozen yogurt and top it with chocolate chips, frozen raspberries, and any of the different treats available. Customers must then weigh their creations and are charged by the weight of their bowls.
Jell E. Bean charges $32 for five pounds of dessert, but not many people buy that much frozen yogurt. She needs you to help her figure out how much to charge her customers. She has customers that are young children who buy only a small amount of yogurt as well as large groups that come in and pay for everyone’s yogurt together.
- Is it reasonable to assume that the weight of the yogurt is proportional to its cost? How can you tell?
- Assuming it is proportional, make a table that lists the price for at least ten different weights of yogurt. Be sure to include at least three weights that are not whole numbers.
- What is the unit rate of the yogurt? (Stores often call this the unit price.) Use the unit rate to write an equation that Jell E. Bean can use to calculate the amount any customer will pay.
- If Jell E. Bean decided to start charging $0.50 for each cup before her customers started filling it with yogurt and toppings, could you use the same equation to find the new prices? Why or why not?
4-48. Lexie claims that she can send 14 text messages in 22 minutes. Her teammates Kenny and Esther are trying to predict how many text messages Lexie can send in a 55‑minute lunch period if she keeps going at the same rate.
- Is the relationship between the number of text messages and time in minutes proportional? Why or why not?
- Kenny represented the situation using the table shown below. Explain Kenny’s strategy for using the table.
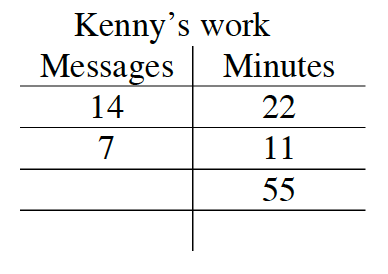
- Esther wants to solve the problem using an equation. Help her write an equation to determine how many text messages Lexie could send in any number of minutes.
- Find the missing value in Kenny’s table.
- Solve Esther’s equation. Will she get the same answer as Kenny?
- What is Lexie’s unit rate? That is, how many text messages can she send in 1 minute?
4-49. Additional Challenge: Use your reasoning skills to compute each unit rate (the price per pound).
- $4.20 for
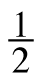 pound of cheese
pound of cheese - $1.50 for
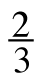 pound of bananas
pound of bananas - $6.00 for
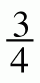 pound of deli roast beef
pound of deli roast beef - $7.50 for
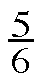 pound of sliced turkey
pound of sliced turkey
Assignment: 4.2.3 Homework

 In the previous lessons, you studied different ways to represent proportional relationships. You organized information into tables and graphs. You also wrote equations modeling the proportional relationships. Proportional relationship equations are of the form y = kx, where k is the constant of proportionality. Today you will find connections between different representations of the same proportional relationship, explore each representation more deeply, and learn shorter ways to go from one representation to another. As you work today, keep these questions in mind:
In the previous lessons, you studied different ways to represent proportional relationships. You organized information into tables and graphs. You also wrote equations modeling the proportional relationships. Proportional relationship equations are of the form y = kx, where k is the constant of proportionality. Today you will find connections between different representations of the same proportional relationship, explore each representation more deeply, and learn shorter ways to go from one representation to another. As you work today, keep these questions in mind:
How can you see growth in the rule?
4-55. Graeme earns $4.23 for each half hour that he works. How much money does he earn during a given amount of time?
- Represent this situation using a table
- What is the constant of proportionality (or the unit rate)? How can you find it from a table?
- How can you use a table to determine if a relationship is proportional?
4-56. Jamie ran 9.3 miles in 1.5 hours. How far can she run in a given amount of time, if she runs at a constant rate?
- Represent this situation with a graph.
- What is the constant of proportionality? How can you find it on a graph?
- How can you use a graph to determine if a relationship is proportional?
4-57. A recipe calls for 2![]() cups of of flour to make two regular batches of cookies. Shiloh needs to make multiple batches of cookies.
cups of of flour to make two regular batches of cookies. Shiloh needs to make multiple batches of cookies.
- Represent this situation with an equation.
- What is the constant of proportionality? How can you identify it in an equation?
- How can you use an equation to determine if a relationship is proportional?
Assignment: 4.2.4 Homework
- Work with a partner to answer Alex’s question.
- Are Alex’s total earnings proportional to the number of weeks he worked? How do you know?
- Why is it important for you to know that miles are proportional to the gallons used?
- Describe the approach you used to complete the table.
- What is the value of the constant? Explain how the constant was determined.
- For which team is distance proportional to time? Explain your reasoning.
- Explain how you know the distance for the other team is not proportional to time.
- If the race were 2.5 miles long, which team would win? Explain.
- If the race were 3.5 miles long, which team would win? Explain.
- If the race were 4.5 miles long, which team would win? Explain.
- For what length of race would it be better to be on Team B than Team A? Explain.
- Using this relationship, if the members on the team ran for 10 hours, how far would each member run on each team?
- Will there always be a winning team, no matter what the length of the course? Why or Why not?
- If the race were 12 miles long, which team should you choose to be on if you wish to win? Why would you choose this team?
- How much sooner would you finish on that team compared to the other team?
Portion Web Practice