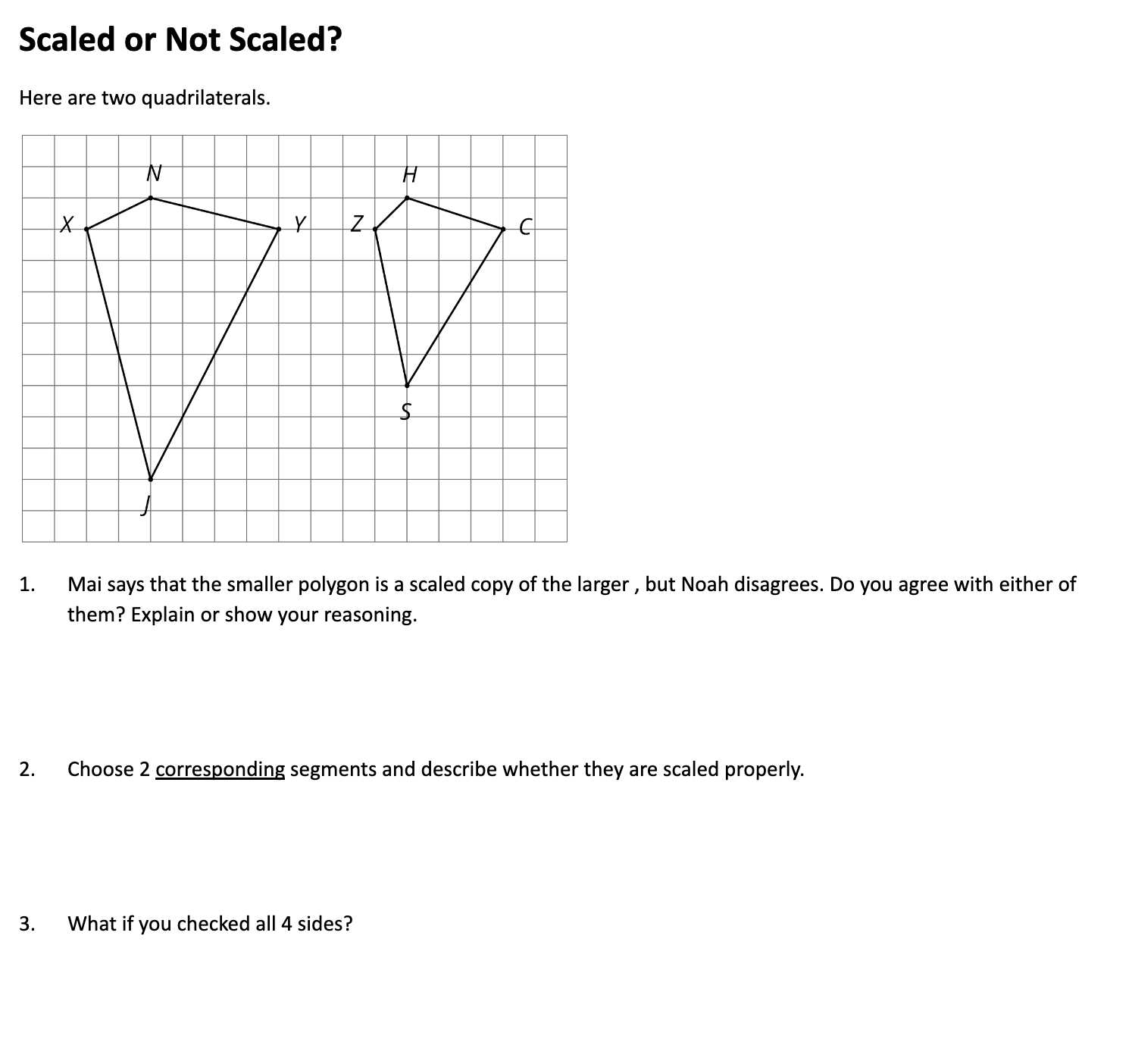
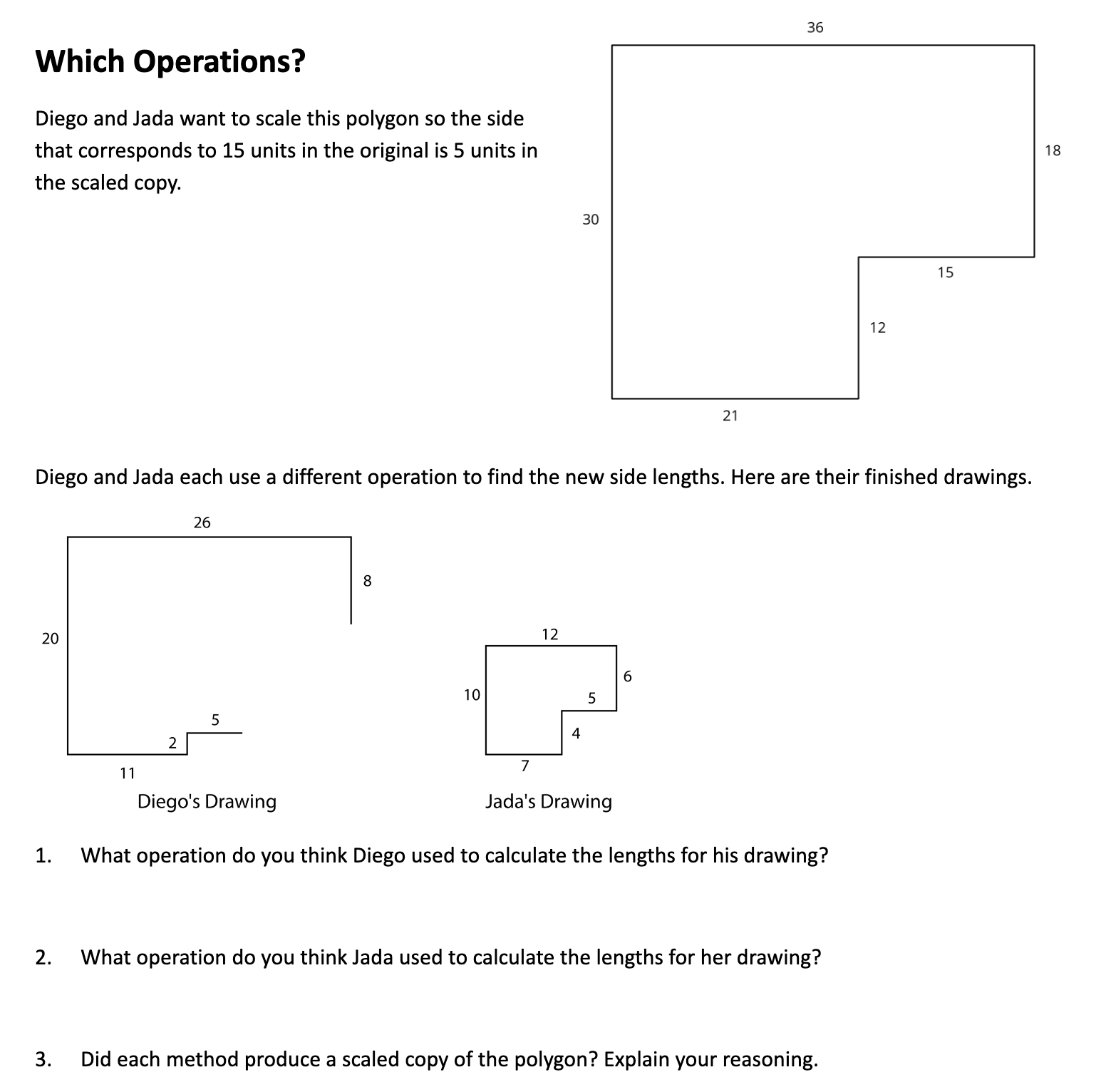
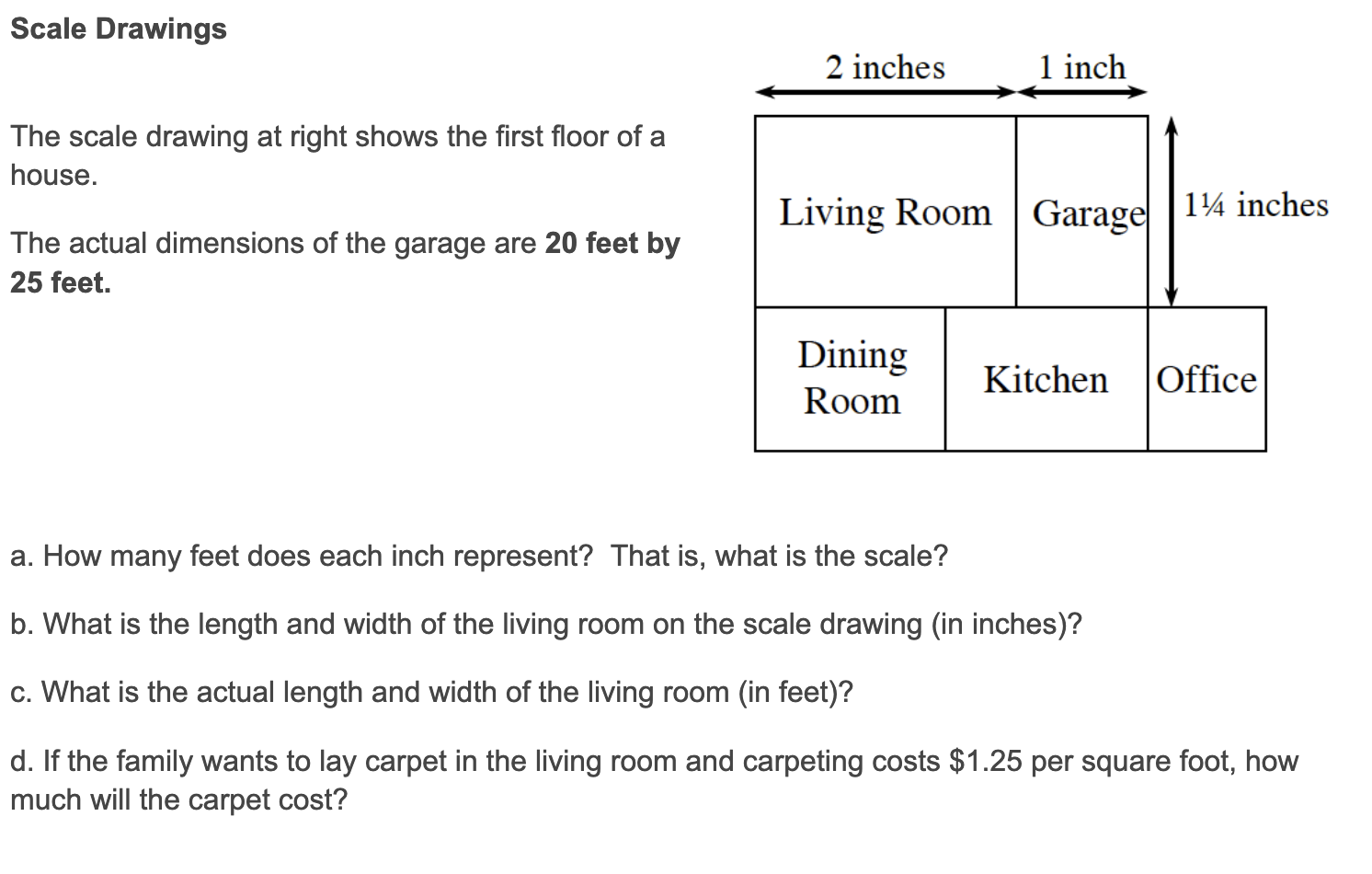
Week 10 – Working with Scale

- How many feet does each unit of the grid represent?
- Use the drawing and scale to find:
- Length of a TYPICAL lawn: _________
- Width of a TYPICAL lawn: _________
- Area of a TYPICAL lawn: _________
- In the grid space above, draw the outline of the BIGGER lawn.
- Use your drawing to find:
- Length of the BIGGER lawn: _________
- Width of the BIGGER lawn: _________
- Area of the BIGGER lawn: __________
- When the length and width double, does the area double as well?
- How many TYPICAL lawns fit inside the BIGGER lawn? How many times bigger is the area?
- Is it a better deal to be paid 3 times the amount for the bigger lawn?
Additional Tasks:
4-12 WB – Guillermo House Scale Drawing
Finding the Scale Factor of Similar Figures – Coloring Activity