[expand title=”Week 3 – Adding Integers”]
 Units of length can be placed one after another in a line to find a measure of an object’s length. Today you will look at how to compose (put together) different lengths to create a new total length.
Units of length can be placed one after another in a line to find a measure of an object’s length. Today you will look at how to compose (put together) different lengths to create a new total length.
2-31. CROSSING THE TIGHTROPE

Cecil is an acrobat in a local circus. His job is to move across a tightrope from point A to point B while blindfolded! He can only move using the distances that you tell him to move in your instructions. He needs to reach the end of the tightrope (point B) to take his bow and go down a ladder. Assume the platforms on both sides of the tightrope extend infinitely (have no end). Cecil may go past the ladder. However, if he does, make sure he turns around and goes back toward the ladder.
Your Task: Work with your team to find different combinations of the lengths given in parts (a) through (e) below that will allow Cecil to move from point A and end at point B (the end of the tightrope). You may use each length as many times as you like.
![]() For each crossing, look for at least three different ways to get the acrobat across. For each solution, draw a diagram on your paper that shows how the available lengths were combined to get Cecil across the tightrope.
For each crossing, look for at least three different ways to get the acrobat across. For each solution, draw a diagram on your paper that shows how the available lengths were combined to get Cecil across the tightrope.
You can find a digital version of this activity at Acrobat Number Line (CPM).
The length strips from the Lesson 2.2.1A Resource Page and Lesson 2.2.1B Resource Page might also be helpful.
a. Span of tightrope: 24 feet Given lengths: 2, 4, 8, 10 feet
b. Span of tightrope: 17 feet Given lengths: 2, 3, 10 feet
c. Span of tightrope: 15 feet Given lengths: 3, 4, 6, 11 feet
d. Span of tightrope: 27 feet Given lengths: 4, 8, 12, 19 feet
e. Span of tightrope: 23 feet Given lengths: 7, 11, 13 feet
2-32. To represent the way that the acrobat could move across a span of 17 feet, Mara wrote the expressions shown below. If each number represents a length in feet, check that each expression would get Cecil exactly to point B. Be prepared to defend each conclusion with a diagram.
- 7 + 3 + 7
- 7 + 10
- 10 + 7
- 10 + 10 + (−3)
- What does the −3 in part (d) represent as a movement for Cecil?
2-33. Write numerical expressions (similar to those in problem 2-32) for each of your solutions to part (c) of problem 2‑31.
Assignment: 2.2.1 Homework
Today you will continue to explore how to combine integer (positive and negative whole numbers and zero) and rational number (fraction and decimal) lengths in multiple ways to find a new length. You will also continue to learn how different combinations can be written with numerical expressions, such as 3 + 3 + (−2) + 11.
2-42. Find the length of the tightrope if each expression for rope lengths below starts Cecil at point A and has him end at point B. Assume the numbers represent lengths in feet.
- 8 + (−3) + 2
- 12 + 7 + (−17)
- 6 + (−3) + (−2)

- 14 + 10 + (−13)
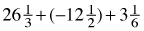

2-43. For Cecil’s new act, his tightrope is 5 feet long.
- If he begins at point A, write two expressions that will make him end at point B. What do these expressions have in common?
- Explain why 5 + 2 + (−2) is equivalent to (the same as) telling Cecil to move 5 feet to the right.
- Will 5 + 2 + (−2) + 2 + (−2) get Cecil to point B? Will 5 + 2 + (−2) + 3 + (−3)? How would you describe his movements in these cases?
2-46. MAKING ZEROS
For Cecil’s newest act, he starts at point A on the left end of his tightrope, walks on the tightrope, turns around, sometimes many times, and then ends up back at point A on the left end of his tightrope.
- Work with your team to write at least three expressions that show how Cecil could move and still start and end at point A.
- Build three more expressions similar to the expressions you wrote in part (a). For your three expressions, do one with two numbers, one with three numbers, and one with eight numbers. What do all of your expressions have in common?
2-49. Consider Cecil’s movements on the tightrope as you answer the questions below.
- What happens when Cecil goes forward 5 feet and then goes back 5 feet? Where does he end up?
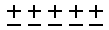 Chad decided to record Cecil’s moves with the diagram at right. Explain what you think his drawing means.
Chad decided to record Cecil’s moves with the diagram at right. Explain what you think his drawing means. Using the same strategy, Chad recorded a different set of instructions for Cecil with the diagram shown at right. What could this diagram represent? How long is the tightrope if these moves end at point B?
Using the same strategy, Chad recorded a different set of instructions for Cecil with the diagram shown at right. What could this diagram represent? How long is the tightrope if these moves end at point B?
2-58. For each expression below:
- Build each expression with + and – tiles
- Sketch each collection of + and – tiles and find the value of the expression.
- Write the solution as an equation.
- Explore using 2-58 Student eTool (CPM).
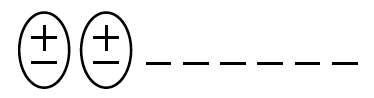 For example, in part (1) below, you might draw the figure at right and record −8 + 2 = −.6
For example, in part (1) below, you might draw the figure at right and record −8 + 2 = −.6
- −8 + 2
- −5 +(−3)
- 2 + (−4)
- −7 + (−7)
- −4 + 3
- −4 + 8 + (−2)
- −3 + 5 + 3
- −6 + 6
2-59. Think about the problems you have worked on involving positive and negative numbers. How would you find the answer to −200 + 14? Without using your calculator, find the sum. Explain your reasoning to your teammates and be prepared to describe your strategy.
Assignment: 2.2.2 Homework

In Lesson 2.2.2, you used integers to represent lengths in two directions. You began to think about using “+” and “–” tiles to represent this forward and backward movement. Today, you will use + and – tiles to model expressions with integers, assigning the + tile a value of one (+1) and the – tile a value of negative one (–1). In your teams, think about these questions as you work:
2-57. WIN-A-ROW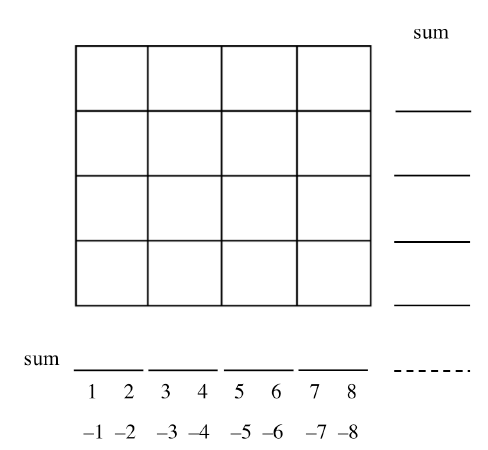
Obtain a Lesson 2.2.3B Resource Page from your teacher or play using the tool: Win-A-Row (CPM). Read the directions for scoring in the game below and play Win-A-Row against a partner.
Scoring: When all the boxes in the table have been filled in, calculate the sum of each row and the sum of each column. Every positive sum means one point for Player 1. Every negative sum means one point for Player 2.
How to Play the Game:
- Play one round of rock-paper-scissors to determine who plays first.
- Player 1 places one of the numbers 1, 2, 3, 4, 5, 6, 7, or 8 in the square he or she chooses and then crosses that number from the list.
- Player 2 places one of the numbers –1, –2, –3, –4, –5, –6, –7, or –8 in another square and then crosses that number from the list.
- Alternate play until all squares are full and all of the numbers have been crossed off the list.
- Add the numbers in each row and write each row’s sum on the appropriate blank in the “Sum” column. Give the winner of each row one point.
- Add the numbers in each column and write each column’s sum on the appropriate blank in the “Sum” row. Give the winner of each column one point.
- If the two players tie after adding the rows and columns, find the sum of the diagonal (from top to bottom and left to right) to decide the final winner.
- If the two players’ sums are still tied, find the sum of the other diagonal (from bottom to top and left to right) to decide the final winner.
- If the game is still tied at this point, both players win!
Ending the Game: The game ends when all squares are full and all sums have been found.
Assignment: 2.2.3 Homework
[/expand]
[expand title=”Week 4 – Multiplying Integers”]
 In previous lessons, you created expressions to help Cecil cross a tightrope. For example, when the tightrope was 16 feet long,you could have written an expression such as 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + (−5) + (−5) + (−5) + (−5) + (−5) + (−5) + (−5) + (−5). When a calculation involves adding the same number over and over, as this one does, is there a shorter way to write the expression? Today, you will consider this as you continue to write and simplify expressions.
In previous lessons, you created expressions to help Cecil cross a tightrope. For example, when the tightrope was 16 feet long,you could have written an expression such as 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 + (−5) + (−5) + (−5) + (−5) + (−5) + (−5) + (−5) + (−5). When a calculation involves adding the same number over and over, as this one does, is there a shorter way to write the expression? Today, you will consider this as you continue to write and simplify expressions.
2-67. Cecil, the tightrope walker introduced in problem 2‑31, still needs your help. He wants to cross a rope that is 6 feet long. Using only the lengths of 5 and 8 feet, find at least two ways Cecil can move to reach the end of the rope at the ladder. For each solution, draw a diagram and write an expression.
2-68. Cecil moved across the rope as shown at right. Show two ways to represent his moves with number expressions. Do both ways get him to the same endpoint?
2-70. When adding the same number several times, multiplication can help. For example, if the tightrope walker moved to the right 3 feet, 3 feet, 3 feet, and then 3 feet, it is shorter to write 4 (3) instead of 3 + 3 + 3 + 3. Note that parentheses are another way to show multiplication. Use multiplication to write 2 + 2 + 2 + 2 + 2.
2-71. How did Cecil, the tightrope walker, move if he started at point A and his moves were recorded as the expression 3(6) + 2? Draw a diagram and record how far along his rope he was when he finished.
2-72. Imagine that Cecil, the tightrope walker, starts at point B and walks on the rope toward point A as shown at right.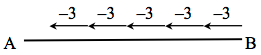
- How should this be written? Is there more than one way?
- Where does he end up?
2-74. The two equal expressions 2(3) and 6 can be represented with the diagram at right. Draw similar diagrams for each of the expressions in parts (a) through (c) below.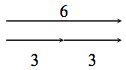
- What does 2(3 + 5) mean? What is the value of this expression?
Describe it with words and a diagram. - What does 2(3) + 5 mean? What is the value of this expression?
Describe it with words and a diagram. - Compare 2(3 + 5) with 2(3) + 5. How are these movements the same or different? Explain your thinking and draw a diagram.
Assignment: 2.2.4 Homework
 You have seen how Cecil’s repeated integer-sized moves can be represented with addition or multiplication. But what if you need to calculate part of a whole? For example, if 200 people enter a competition and
You have seen how Cecil’s repeated integer-sized moves can be represented with addition or multiplication. But what if you need to calculate part of a whole? For example, if 200 people enter a competition and 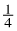 of them are chosen for the final round, how do you calculate how many were chosen? Sometimes you may even need to calculate a part of a part. For example, if Cameron sprinted
of them are chosen for the final round, how do you calculate how many were chosen? Sometimes you may even need to calculate a part of a part. For example, if Cameron sprinted  of the
of the 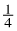 -mile track, how would you calculate how far Cameron sprinted? Today you will use different models to help you answer these kinds of questions.
-mile track, how would you calculate how far Cameron sprinted? Today you will use different models to help you answer these kinds of questions.

2-85. Cecil has just created a spectacular routine. (A routine is a sequence of moves to get from start to finish.) His routine has two parts. The first part consists of a series of creative leaps followed by a somersault. The first part ends with Cecil’s doing an elaborate bow while balancing on one toe. Then he moves into the second part of the routine, which includes several back flips and spins. When performed perfectly, the routine moves Cecil exactly to the other end of his tightrope. The routine can be represented by the following expressions. First,
Part I: 3(2) + 3(3) + (−5) + 4
Then he pauses to take a bow in place. And then,
Part II: 5 + 3 + 4(1 + −1) + (−3) + (−5) + 3(5 + (−2)) + 1
Work with your team to draw an accurate diagram (drawn to scale) to represent Cecil’s routine. Then answer the following questions and be ready to share your reasoning. Assume that the numbers used to describe the routine represent feet. How long is Cecil’s tightrope? How far from the starting point is Cecil when he takes his bow after Part I?
- How long is Cecil’s tightrope? How far from the starting point is Cecil when he takes his bow after Part I?
- What portion of the tightrope length does Cecil travel in each part of the routine?
- Cecil had only completed two thirds of his routine when a rather violent sneeze caused him to fall. How far from the starting point was Cecil when he sneezed and fell?
Assignment: Adding Subtracting Integers Word Problems
2-86. Garden Road Middle School is planning a field trip for students to attend a conference about careers in mathematics. Half of the students signed up to go on the field trip, but only three fourths of those students brought back their permission slips to attend the field trip. Explore what fraction of students in the school will be able to go on the field trip.
- Discuss this problem with your team. Do you have to know how many students go to Garden Road Middle School to be able to answer this question? Why or why not? Once you have reached agreement on this issue, ask your teacher for a Lesson 2.2.5 Resource Page, called “Unit Rectangles,” or draw eight identical rectangles on a full sheet of paper. Then follow the steps below to answer the question.
 The entire school’s enrollment—no matter what it is—can be represented with an unshaded unit rectangle, as shown at right.
The entire school’s enrollment—no matter what it is—can be represented with an unshaded unit rectangle, as shown at right.
Half of the school plans to attend. To show this, divide your rectangle into two equal pieces, as shown below. Then lightly shade and label one of the halves to show the half of the school that is planning to attend.
Label the other half with an appropriate label.- Three fourths of the students planning to attend brought back their permission slips to go to the conference. Represent this portion on your rectangle.
- What fraction of the whole school will attend the conference?
- If the total school population is 120 students, how many would attend?
- Additional Challenge:How do you know that the total school population cannot be either 125 or 250?
Assignment: 2.2.5 Homework
[/expand]
[expand title=”Week 5 – Mixed Integers”]
 In previous lessons you have worked with expressions, combinations of numbers, variables, and operation symbols,that involve either adding integers or multiplying integers. Today you will examine expressions that involve both operations. By the end of this lesson, you will be expected to be able to answer these target questions:
In previous lessons you have worked with expressions, combinations of numbers, variables, and operation symbols,that involve either adding integers or multiplying integers. Today you will examine expressions that involve both operations. By the end of this lesson, you will be expected to be able to answer these target questions:
How can expressions with the same numbers and operations
have different meanings?
Does the order in which we do each operation matter?
3-1. Katrina wrote the following set of instructions for Cecil: 4 · 2.5 + 1.
1. If Cecil the acrobat follows Katrina’s instructions, how far will he go? Draw a diagram of Cecil’s movements and show how far he will move.
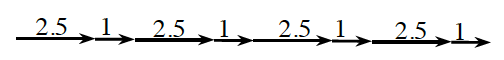
2. Katrina drew the diagram at right. How was she thinking about Cecil’s moves? Write an expression to represent Katrina’s diagram.
3. Explain why Katrina’s diagram in part (b) will not give her the correct length for 4 · 2.5 + 1.
4. Cecil changed Katrina’s set of instructions so that the length of 1 foot came first, as shown in the diagram at right. Write an expression to represent this new diagram. How far does Cecil move here? Does this give the same length 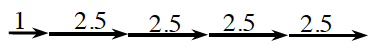 as 4 · 2.5 + 1?
as 4 · 2.5 + 1?
3-2. Cecil’s trainers proposed each of the following movements. Which one requires the longest rope? Draw diagrams to justify your answer.
- 8 + 2(6.48) feet
- 2 + 8(6.48) feet
- (8 + 2)6.48 feet
3-3. The expression 5 + 3 · 4 + 2 can be used to represent the group of + t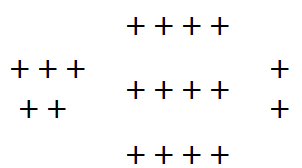 iles shown at right.
iles shown at right.
- Work with your team to explain how each part of the expression connects with the groups of + tiles. How many tiles are there?
- Each group of + tiles is represented by a different part of the expression, also called a numerical term. Numerical terms are single numbers or products of numbers. It is often useful to circle terms in an expression to keep track of separate calculations. For example, each term circled in the expression below represents a separate part of the collection of + tiles above.

Circle the terms in the expression shown below. Then explain what each term could describe about collections of + or – tiles.
4 · 5 + 1 + 3(–2) + 6
3-4. Circle the terms and simplify each expression shown below. Simplify means to write an expression in its simplest form. In the case of numerical expressions, the simplest form is a single number.
- 7.08 + 2.51 + (−3.84)
- 7.8 + 2.1(−3)
- 5(−
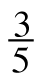 )+ 2 · 1.5
)+ 2 · 1.5 - 4.35 · 2 + 5 +3
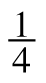 (−1) + (−10)
(−1) + (−10)
Assignment: 3.1.1 Homework

In today’s lesson, you will continue to simplify expressions using the correct Order of Operations. You will also learn how to identify terms in expressions that are more complicated.
3-14. Consider the expression 3(5 + 2 · 4) + 2(−3).
- Work with your team to draw a diagram representing this expression. Your diagram could show Cecil’s movements, for example, or it could show + and – tiles that could be represented by this expression.
- Simplify the expression.
- Discuss with your team how you might circle terms in this expression. Be ready to explain your ideas to the class.
3-16. AIM FOR 16
- In this game, you and the other players will create expressions that contain the same four numbers. Then you will compare the numbers that your expressions represent to see whose number is closest to 16.
- Your teacher will roll four number cubes or use 3-16 Number Cubes (CPM) to virtually roll four number cubes to determine the four numbers you can use in your expression. You may use each number as either a positive or negative integer, and each number must appear exactly once in your expression. For example, if a number cube lands on 5, you can use either 5 or −5 in your expression. Try to make an expression that represents a number that is as close to 16 as possible.
- Your score is how far your expression’s value is from 16. For example, for an expression that represents 20, the score would be 4, and for an expression that represents 13, the score would be 3. Compare your expression with your opponent’s. Whoever has the lowest score wins that round. As you continue playing more rounds, keep track of your total score and try to keep it as low as you can.
3-17.Additional Challenge: Simplify each of the expressions below. For each one, be sure to show your work or explain your reasoning.
- (4 + 2(−5) + 3(2 + (−3)) + 2) 6 + (−2)
- (9 + 3(−2 + 4)) + (6 + 2(5 + (−7)) + 1)
Assignment: 3.1.2 Homework

In Chapter 2, you worked with adding and multiplying integers (positive and negative whole numbers and zero). In this lesson, you will use + and – tiles to learn about subtraction of integers. Keep the following questions in mind as you work with your team today. At the end of the lesson, you will discuss your conclusions about them.
How can we remove negative tiles when the collection has only positive tiles?
How can we think about subtraction when there are not enough to “take away”?
When does subtracting make the result larger?

3-24. Examine the assortment of positive and negative tiles at right. What integer does this assortment represent? Explore using the 3-24 Student eTool (CPM).
- What happens if three + tiles are removed? How can you use numbers and symbols to represent this action and the resulting value?
- What happens if three – tiles are removed from the original set of tiles? Again, how can you represent this action and the result using numbers and symbols?
3-25.
- −8 −(−3)
- It is cold! The first time I looked at the thermometer today, it said it was 0 degrees Fahrenheit. Then it dropped 5 degrees! How cold is it now?
3-26. For each of the expressions below find the difference:
- 7 − 5
- 0 − 4
- −6 − 2
- 3 − (−4)
- −8 − (−5)
- −1 − (−9)
3-27. Subtraction can also be represented on the number line model.
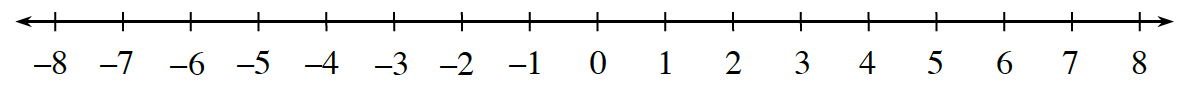
- Sketch the number line above on your paper.
- How can you represent 2 − 7 using the number line? Discuss your ideas with your team and use the number line to represent your answer.
- How can you represent 1 − (−2) using the number line? Again, discuss your ideas with your team and use the number line to represent your answer.
3-32. Additional Challenge: Add parentheses to make each subtraction equation true.
- 1 − 3 − 5 − 7 = 0
- 1 − 3 − 5 − 7 = −14
- 1 − 3 − 5 − 7 = −4
- 1 − 3 − 5 − 7 = 10
Assignment: 3.1.3 Homework
[/expand]
[expand title=”Week 6 – Integers Continued”]

In this lesson, you will work with your team to continue thinking about what happens when you remove + and – tiles from a collection of tiles representing a number. You will extend your thinking to find ways of making your calculations more efficient when the same number of tiles are removed multiple times. Consider these questions as you work today:
adding and multiplying integers in Chapter 2?
3-53. Troy and Twana are working with the expression −10 −(−2) − (−2) − (−2)
- Help them find a shorter way to write this expression.
- Imagine that their expression does not include the –10. How could they write the new expression? What number would this new expression represent?
3-54. How could you evaluate the product −7(−11) ? Work with your team to make sense of −7(−11) .
3-55. WHAT DOES IT MEAN?
Your Task: Work with your team to find the following products:
| 4(−3) | −4(−3) | −4(3) |
| 2(−7) | −2(−7) | −2(7) |
3-57. What does −18 ÷ 9 equal? How do you know? Explain why your answer makes sense. Then complete the division problems below.
- 45 ÷ (−3)
- −32 ÷ (−8)
- −54 ÷ 6
Assignment:3.2.3 Homework

In this lesson, you will have an opportunity to practice adding, subtracting, multiplying, and dividing integers as you play a game against a partner. As you play, consider these questions:
Which operation with these integers will move us farthest?
3-78. TUG-O-WAR
Obtain a Lesson 3.2.5 Resource Page from your teacher or use the Tug-O-War eGame (CPM) and play Tug-o-War against your partner. Keep track of any strategies that you use or discover as you are playing. Play until your teacher calls time. The rules are printed below.
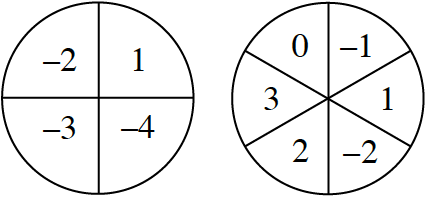
How to Play
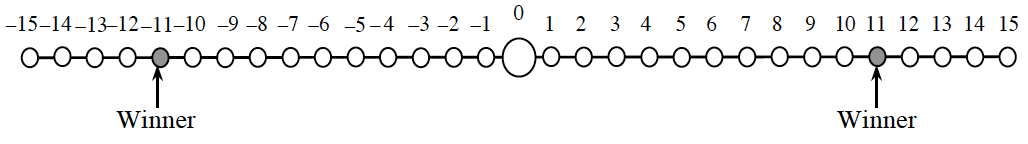
3-79. With your team and then as a class, discuss any strategies that you used or discovered as you played the Tug-o-War game. Use the focus questions at the beginning of this lesson to guide your discussion.
3-80. Cynthia, Devin, Gavin, and Mark are playing the Tug-O-War game.
- Cynthia begins her turn with her marker at 15. She spins a 1 and a –3. She thinks that she might be able to get to the winner space at 11 with this spin. Is she correct? Explain why or why not.
- Devin takes his turn. His marker is on the 1, and he spins a 4 and a –3. Is it possible for Devin to get to one of the winner spaces (at 11 and –11) with these numbers? Explain your answer.
- Gavin now has his marker at 12, and he spins a –3 and a –2. Gavin is wondering if he can win on this turn. Can he? Explain your answer.
- Mark is currently at −14 and spins a −3 and a −1. He sees a way to win. How can he do this? Is there more than one way? Explain your answer.
3-81. Roger went home to play the Tug-o-War game with his older brother, Hank. Hank looked at the spinners, thought for a bit, and then told Roger that the game is flawed because you cannot get all of the integers from −10 to +10. Roger wondered if Hank was right.
Are there any integers from −10 to +10 that you cannot get using any of the operations with the results of a spin on each spinner? Do you think that this would make the game unfair or flawed? Work with your team to build a convincing argument that demonstrates whether or not Hank’s claim is true.
Assignment: 3.2.5 Homework

Remember when operations with numbers were simple? In elementary school, you learned to add, subtract, multiply, and divide whole numbers. As you have seen, there is a lot to consider when operating with different kinds of numbers. In this lesson, you will put together much of your understanding of operations with integers and simplifying numerical expressions to draw conclusions about order and grouping of operations.
3-112. Juno was working on simplifying the expression 24 + 3 +(−4) + 7. “I know!” he exclaimed. “It must be equal to 30, because 20 plus 10 is 30.”
- Is Juno correct? Is the value of the expression 30?
- How could Juno have found 20 and 10 in this expression? Discuss this with your team and be prepared to share your ideas with the class.
3-113. In problem 3-112, Juno used his understanding of two different properties: the Commutative Property of Addition and the Associative Property of Addition. The Commutative Property of Addition allows Juno to rearrange 24 + 3 + (−4) + 7 into a different order, such as 24 + (−4) + 3 + 7. The Associative Property of Addition allows him to group numbers in different ways, so instead of adding from left to right, he can add in two groups and then combine them like this: (24 + (−4)) + (3 + 7) = 20 + 10 = 30.
3-114. Consider expressions involving addition and subtraction, such as 7 − 2 + 4.
- Work with your team to calculate the value of this expression. Be prepared to explain your method to the class.
- Does the grouping matter? In other words, is (7 − 2) + 4 the same as 7 − (2 + 4)? Explain.
- Does order matter? In other words, is 7 − 2 + 4 the same as 2 − 7 + 4? Explain.
- In expressions that involve addition and subtraction, in what order should those operations be calculated? Consider the following expressions to help you think about this.
- 10 − 2 + 4
- 3 − 5 − 2 + 6
- 7 − 3 − 2
3-115. Juno has another idea. “Wait!” he says. “Can’t subtraction be rewritten using addition? Since order doesn’t matter when we add, can’t we just rewrite the subtraction as addition so we can use any order?”
Discuss Juno’s idea with your team and then rewrite each of the following expressions so that each one involves only addition. Then use the fact that the numbers are all being added and the order can be changed to find a way to simplify each expression efficiently.
- 17 − 4 − 11 + 15
- 2 − 2 · 3 − 4 − 2(−4)
3-117. Additional Challenge: Use each integer –6, 2, –3, and 1 once with any of the four operations or parentheses to make:
a. The largest possible answer.
Zero or the closest number to zero.
The smallest possible answer.
Assignment: 3.3.3 Homework
[/expand]