Concept 1 – Introduction to Probability

[expand title=”Week 1 – Experimental or Theoretical Probability?”]

Certainty

Write a short statement or sentence for each of the following:

Think of something that certain or guaranteed to happen
Think of something that is impossible, or could not happen
Now, think of something in between

You have probably heard a weather forecaster say that the chance of rain tomorrow is 40%. Have you thought about what that means? Does it mean that it will rain tomorrow for sure? What is the chance that it will not rain? In today’s lesson, you will investigate the chance, or the probability, of something happening or not happening. As you do the activities, ask your team these questions:

What is the probability of the event occurring?

How can we record that probability?

1-51. GO FISH

Mike wants to win a giant stuffed animal at the carnival. He decided to play the “Go Fish” game, which has three prizes: a giant stuffed animal, a smaller stuffed animal, and a plastic kazoo.

The game is set up with a tank containing 1 green fish, 3 blue fish, and 6 yellow fish. To play, Mike must go fishing. The game is set up so that every time a player goes fishing, he or she will catch a fish. Simulate the game by creating a bag with tiles matching the fish colors using the 1-51 Student eTool.

To win the giant stuffed animal, Mike needs to catch a green fish.

If all of the fish in the tank are green, how would you describe the probability of Mike’s winning a giant stuffed animal?
The way the tank is set up (with 1 green, 3 blue, and 6 yellow fish), what are the chances that Mike will catch a black fish?
Given the information in the problem, what percent of the time would you expect Mike to catch a green fish and win the giant stuffed animal? Be ready to explain your thinking.

1-52. In the game described in problem 1-51, you could expect Mike to win a giant stuffed animal 10% of the time. A percentage is one way to express the probability that a specific event will happen. You might also have said you expected Mike to win 1 out of every 10 attempts. So the probability that Mike will win is , because the 1 represents the number of desired outcomes (green fish that Mike can catch) and the 10 represents the number of possible outcomes (all the fish that Mike could catch).

What is the probability that Mike will catch a blue fish? A yellow fish? Write each of these probabilities as a fraction and a percent.
Probabilities such as the ones you found in part (a) are called theoretical probabilities because they are calculated mathematically based on what is expected.What is the theoretical probability of getting a fish that is green, blue, or yellow (that is, a fish that is any of those three colors)? How do your answers for this problem compare to the probabilities you considered in problem 1-50?

Theoretical Probability is a calculated probability based on the possible outcomes when they all have the same chance of occurring.

Theoretical Probability =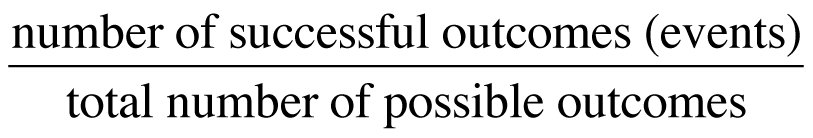

WB – Portion Web

1-63. THE MYSTERY SPINNER

Your teacher has a hidden spinner. Your challenge is to perform an experiment that will allow you to predict what the spinner looks like without ever seeing it.

Your Task: Your teacher will spin the spinner and announce each result. During the experiment, you will consider several questions about the results and about the hidden spinner. However, you will not be allowed to see it. Using the information you get, work with your team to figure out what the spinner looks like. When you think you know what it looks like, draw a diagram of the spinner.

1-64. Use the data you collected in problem 1-63 to answer the following questions.

Based on your data, how can you describe the likelihood of landing on each part of the spinner? How does the spinner that your team drew represent these likelihoods? Be prepared to share your ideas with the class.
Use your data to write the experimental probability of each of the following results as a fraction, a decimal, and a percent.
1. The spinner lands on purple.
2. The spinner lands on green or orange.
If your teacher were to spin the spinner 15 more times, how might this change your answers for part (b)?
Do you know for sure that the spinner you drew in problem 1-63 looks exactly like your teacher’s? Are you certain that the portions that you drew for each color are the same size as the portions on your teacher’s spinner? Why or why not?

1-65. Now your teacher will reveal the mystery spinner.

How does your team’s spinner compare to the actual spinner? Discuss the similarities and differences.
Do your spinner and your teacher’s spinner show the same likelihood for each section being spun? Explain why or why not.

1-66. One way to compare your spinner and your teacher’s spinner is to calculate the theoretical probability for each colored section of your teacher’s spinner.

What are some reasons the experimental probability and the theoretical probability for any section of the spinner could be different?
Estimate the theoretical probability for getting each color on your teacher’s spinner.
How do the experimental probabilities (based on your class data) and the theoretical probabilities (based on the actual spinner) compare? How do you think they would compare if there were twice as many spins made? What about three times as many spins?
If you were to spin the spinner the number of times listed below, how many times would you expect it to land on orange? Explain how you found your answers.
1. 6 times
2. 48 times
Approximately how many times would you expect to land on orange if you were to spin 100 times?

Assignment: 1.2.2 Homework

If you want to have the best chances of getting a red gumball from a gumball machine, is it better if the machine is full of gumballs or half empty? How do the chances of getting an ace in a deck of playing cards change if you have three or four decks of cards to choose from instead of only one deck? In this lesson, you will think about the size of the sample space (the collection of all possible outcomes of an event). Think about these questions as you work today:

How has the “whole” or total changed?

How has the “portion” or part we are interested in changed?

Has the event become more or less likely?

1-75. We have a bag containing a set of colored blocks or counters, or 1-75 Student eTool (CPM). The bag contains 1 yellow, 2 red, 4 green, and 5 blue blocks.

Are we working with Experimental or Theoretical probability?
Look at the blocks in your bag. If you were to reach into the bag and select one block without looking, what is the likelihood that it would be:

Red?
Green?
Blue?
Orange?

1-76. If you were to select one block from the bag 12 times, replacing the block you drew between each selection, how many of those times would you expect to have selected a blue block? What if you drew 24 times? Discuss both situations with your team and explain your answers.

Do you think the larger sample space will change the likelihood of drawing blocks of different colors?

1-78. In problems 1-75 through 1-76, even though you combined bags or changed the number of selections you made, the probability of drawing a blue block remained the same.

Do you think the probabilities would change if you combined three bags? Why or why not?
What change do you think you could make in order to increase the chances of choosing a blue block? Explain your reasoning.

Assignment: 1.2.3 Homework

[/expand]

[expand title=”Week 2 – Compound Probability”]

So far in this section, you have worked with probabilities involving one specific desired outcome. Now you will investigate probabilities of compound events. Compound events are events with combinations of outcomes. In today’s lesson, you will find the probability that either one of the events or the other event occurs. (In Chapter 5, you will consider the probability that both one event and another event occur.)

Think about these questions as you work with your study team:

How is this probability related to the probability of a single event?
Either what event or what other event are we interested in?
Does our answer make sense?

1-119. Thomas helps around the house by doing one chore after school. Each day, Thomas and his aunt use the spinner at right to decide which chore he will do. Here is what Thomas knows: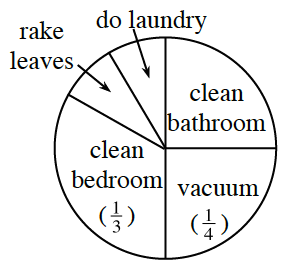

The sections on the spinner for “rake leaves” and “do laundry” are the same size.
The sections for “clean bathroom” and “vacuum” are equal in size and together make up half the spinner.
Explore the 1-119 Student etool (CPM) to help you answer the questions below.

What is the probability that Thomas will spin “do laundry”?
Thomas hates to clean the bathroom. When he spins the spinner, what is the probability that it will not point to “clean bathroom”? Explain how you found your answer.

1-120. Thomas’s aunt hopes that he will either spin “clean bedroom” or “rake leaves” today.

What is P(clean bedroom)? What is P(rake leaves)?
Spinning either chore in part (a) would make Thomas’s aunt happy. With your study team, discuss the questions below and record your team’s answers. Be sure to justify your conclusions.
- What is the probability that he will spin either one of the chores?
- How can you write the two outcomes as a single probability?

1-121. Ms. Nguyen lets her students borrow pens and pencils on days when they have a quiz. She has a paper bag containing hundreds of wooden pencils, mechanical pencils, and blue pens.

Stuart forgot his pencil, and it is quiz day! Ms. Nguyen tells him that one out of every three students who reaches into the bag pulls out a wooden pencil. Two out of every five students pull out a mechanical pencil. The rest of the students pull out a blue pen.

If Stuart reaches into the bag without looking, is it more likely that he will choose a wooden pencil or a mechanical pencil? Justify your thinking.
How can you describe the probability that Stuart will pull out some kind of pencil—either a wooden pencil or a mechanical pencil—by using the probabilities that you already know? Consider what you know about adding and subtracting fractions and see if you already have a strategy to write this probability as a single number.

1-122. Felicia was trying to find the probability that she would pull either a wooden pencil or a mechanical pencil out of Ms. Nguyen’s bag from problem 1-121. “I think I need to combine the probability that I will get a wooden pencil with the probability that I will get a mechanical pencil,” she said. She set up this expression and drew a picture:

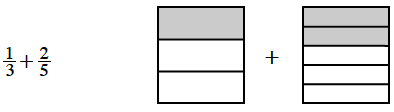
Felicia wondered if she could add the parts. Is the sum 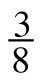? Why or why not?
Discuss with your team how Felicia could change the way she writes each fraction so that she can add them easily. Be ready to explain your reasoning. Then, find the sum.

Assignment: 1.2.7 Homework

Pick a Tile

Gina has a bag containing Red, Green, Blue, Yellow, and White tiles.
If someone picks a tile without looking:
• The probability of picking a Red tile from the bag is one half.
• The probability of picking a Green tile is half the probability of picking a Red tile.
• Blue, Yellow, and White tiles have an equal probability of being picked.

Use this information to complete the table.

Pick a tile (Mars) Revised

WB – Compound Spinner

Roberto was playing a game that required spinning a spinner. On his first ten spins, he landed on four different spaces. He landed on:

Lose a Turn one time

Move Forward One Space four times

Move Forward Two Spaces three times

Move Back One Space two times

Based on this data, what is the probability that Roberto will spin Move Forward Two Spaces on his next spin? Why?
Based on this data, what is the probability he will NOT land on Move Back One Space on his next spin? Why?
Based on this data, what do you think this spinner looks like? Justify your statements.

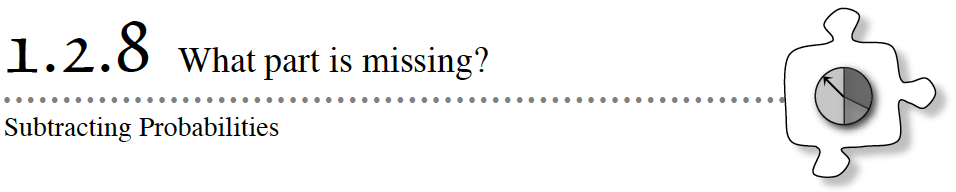
In Lesson 1.2.7, you calculated probabilities for single events and combinations of events when either one outcome or the other is desirable. You have also compared those probabilities to decide which outcomes are most likely. In this lesson, you will work with your study team to apply your knowledge of fractions to represent and calculate the probabilities of a variety of events. As you work today, ask each other these questions to focus your discussion:

How can probabilities be combined?

How can the answer be rewritten in a different form?

1-131. Lindsay has a paper bag full of Fruiti Tutti Chews in three different fruit flavors. She says, “If you reach into the bag, you have a chance of pulling out a Killer Kiwi. There is a chance that you will get Crazy Coconut.”

If you reach into the bag, what is P(coconut or kiwi)?
Does there have to be another flavor in the bag? How can you tell? If so, assuming that there is only one other flavor, what is the probability of getting that flavor?
How many candies might Lindsay have in the bag? Is there more than one possibility? Assume that all candies in the bag are whole candies.

1-132. Lyle asked for a challenge problem, and his teacher gave him this one:

There is a chance of drawing a red marble out of a bag of marbles. If the probability of drawing a red or a blue marble is , what is the probability of drawing a blue marble? You may want to use the Probability eTool to simulate this problem.

When Lyle’s teammates saw the challenge he was working on, they each had a different idea for how he should start.

Mayra suggested that he start by rewriting 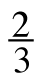and 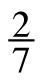so that they have a common denominator.
Kenessa disagreed. “You want to set up a subtraction problem,” she said. She wrote the expression 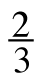− 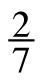to show the number Lyle needs to find.
Darren had a different idea. “The probability that you would draw either red or blue is the same as the probability of drawing red added to the probability of drawing blue,” he said. He wrote this expression:
+ ? =

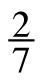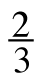
Which way would you suggest Lyle start working to find P(blue)?
- Discuss your ideas with your study team.
- Write a clear explanation of which method you recommend and why.
- Include your ideas about whether the other strategies will solve the problem and why you did not choose them.
What is the probability of drawing a blue marble? Explain your reasoning

1-134. Charles found a spinner his teacher was making. 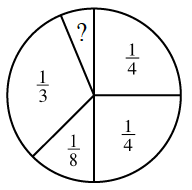He knew that if he put his problem-solving skills to use, he would be able to figure out the missing piece and finish the spinner for his teacher.

Write an expression for the problem Charles needs to solve. Is there more than one way to do this?
Find the solution.

Assignment: 1.2.8-homework

[/expand]