[expand title=”Using cups and counters to model equations”]
One Step Expressions
Assignment: Problem Set – Equations – 1 step cups
Multiplication and Division
Assignment: Equations – 1 step cups Mult and Div
Rational Numbers
Assignment: One-Step Equations With Fractions
[/expand]
[expand title=”Multi-step equations”]
Modeling Equations with Cups and Counters – Glencoe
Assignment: Two-Step Equations With Integers
Variables on both sides (7.EE.4)
What do you do when there are variables on both sides of an equation?
Example 1
- x + 1 = 2x – 5
- 3x + 6 = – x + 2
- 6x + 6 = – 4x + 86
- 7x + 1 = 2x + 41
Exercise 1
| 1.) 5x + 8 = 57 – 2x | 2.) 7x + 9 = 45 + 3x |
| 3.) x + 7 = – 6x + 21 | 4.) – 4x + 1 = 13 – 3x |
Assignment: Multi-step variables on both sides
[/expand]
[expand title=”Representing situation with equations”]
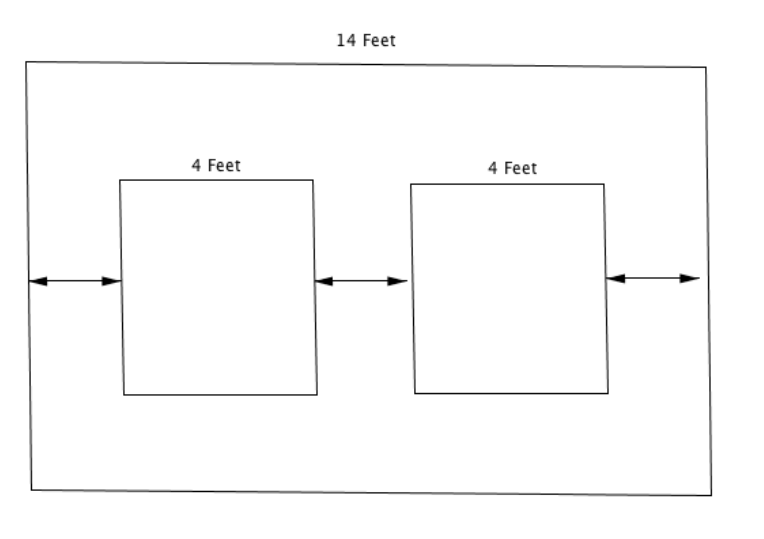
Your brother is going to college, so you no longer have to share a bedroom. You decide to redecorate a wall by hanging two new posters on the wall. The wall is 14 feet wide and each poster is four feet wide. You want to place the posters on the wall so that the distance from the edge of each poster to the nearest edge of the wall is the same as the distance between the posters, as shown in the diagram below. Determine that distance.
Exercise 1
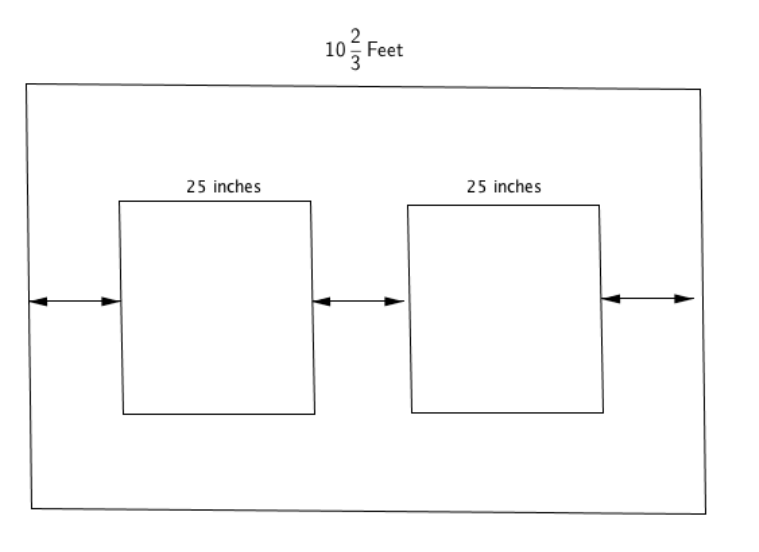
Your parents are redecorating the dining room and want to place two rectangular wall sconce lights that are 25 inches wide along a 10 foot, 8 inch wall, so that the distance between the lights and the distances from each light to the nearest edge of the wall are all the same. Design the wall and determine the distance.
Let the distance between a light and the nearest edge of a wall be x ft. Write an expression in terms of x for the total length of the wall, and then use the expression and the length of the wall given in the problem to write an equation that can be used to find that distance.
Now write an equation where y stands for the number of inches: Let the distance between a light and the nearest edge of a wall be y in. Write an expression in terms of y for the total length of the wall, and then use the expression and the length of the wall (in inches) given in the problem to write an equation that can be used to find that distance (in inches).
What value(s) of y makes the second equation true: 24, 25, or 26?
Exercise
1. Sophia pays a $19.99 membership fee for an online music store.
a. If she also buys two songs from a new album at a price of $0.99 each, what is the total cost?
b. If Sophia purchases n songs for $0.99 each, write an expression for the total cost.
c. Sophia’s friend has saved $118 but isn’t sure how many songs she can afford if she buys the membership and some songs. Use the expression in part (b) to write an equation that can be used to determine how many songs Sophia’s friend can buy.
d. Using the equation written in part (c), can Sophia’s friend buy 101, 100, or 99 songs?
Exercise 2
Check whether the given value is a solution to the equation.
a. 4n − 3 = −2n + 9 n = 2
b. 9m − 19 = 3m + 1 m =
d. 3(y + 8) = 2y − 6 y = 30
[/expand]
[expand title=”Equations Assessment”]
Expressions and Equations Quiz
[/expand]