Quadratic Functions – Paine in the Math

Making sense of quadratic functions by examining their graphs

[expand title=”Graphing Quadratic Functions”]

Introduction: Will it hit the hoop?

Collecting data: Penny Circle

Introduction: Dan Meyer – Penny Circle

http://vimeo.com/44558245

Materials:

Compass
50 pennies

Instructions:

Step 1: Draw 5 circles using a compass. Use diameters 1, 2, 3, 4, and 5 inches. Place as many pennies as you can in each circle, making sure that each penny is completely within the circle (Penny Circles)
Step 2: Record your findings in a table like the one shown. Also include a prediction for the number of pennies that would fit in a circle with a diameter of zero inches.

[ezcol_2fifth]

[/ezcol_2fifth][ezcol_3fifth_end]

[/ezcol_3fifth_end]

Step 3: Make a scatter plot of your predictions. Fit a line to your scatter plot. Describe what your line looks like.
Step 4: Use your graph to predict how many pennies will fit in a 6 inch circle. Then, Draw a 6 inch circle and test your prediction. How reasonable was your prediction?
Beyond: Predict how many pennies will be in the huge circle in the video.

[/expand]

Examining the structure of a quadratic function and relating it to its graph.

[expand title=”Getting to know Quadratics”]

Desmos:

Polygraph
Marbleslides

What is a quadratic function?

First, what is a function? (Hint: it is in your notes). A function defines a relation for which each input has one (and only one) output.

So a quadratic function is a still a relation for which each input has one output, except the rule which defines the relation contains a variable that is squared. It is said to have a degree of 2.

Ex:

$f(x)= x ^{2}$

$f(x)= 5x ^{2}$

$f(x)= x ^{2}+x+1$

Write your own quadratic function…

What to know about quadratic functions

The name quadratic comes from “quad” meaning square, because the variable gets squared (such as $x ^{2}$ ).

A quadratic function is a function in the form:

$f(x)=a x ^{2}+bx+c$

Where a, b, and c are real numbers and a is not equal to zero.

What are some examples of real numbers?
Why cannot a be equal to zero?

So, what do a, b, and c do? Lets have a look…

The Simplest Quadratic: $f(x)=x ^{2}$ and its graph:

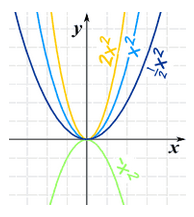
When we introduce the “a” value: $f(x)=ax ^{2}$

Larger values of a squeeze the curve
Smaller values (closer to zero) of a expand the graph
And negative values of a flip it upside down

[/expand]

Using the different forms of quadratic functions

[expand title=”The Different Forms of Quadratics”]

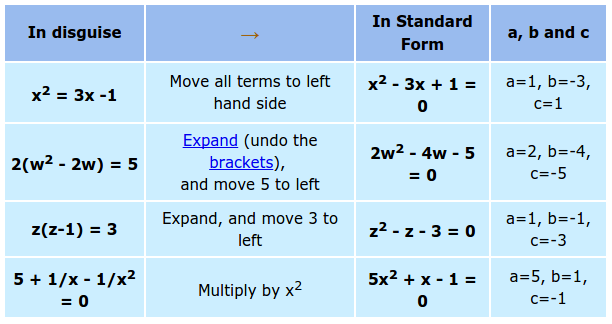
A quadratic function is a function in Standard Form: (Yes, you have seen this before). This is the most common way of writing a quadratic function.

$f(x)=ax^{2}+bx+c$

Where a, b, and c are real numbers and a is not equal to zero.

Sometimes a quadratic is not in standard form, but it is still a quadratic. For example:

We can also write them in Vertex Form.

$f(x)=a(x-h) ^{2}+k$

But first, what is a vertex?

The vertex is the point representing the maximum or minimum of a parabola, depending of it is opening up or down.

We can convert from standard for to vertex form

Converting between standard form and vertex form

First, why would we use vertex form? Well, h and k represent the maximum or minimum, so if we know that point, we can graph the function easier.
Also, the curve is symmetrical (mirror image) about the axis that passes through

x = h

How do we find h and k?

$h=\frac{-b}{2a}$ and $k=f(h)$
Find h, then solve f(h) to find k

Day 2 Assignment:

Converting and Graphing Vertex Form

[/expand]

[expand title=”Practice with Quadratics”]

PH 9-2
- Axis of symmetry
- Graphing quadratics from standard form
- Graphing quadratic inequalities
- Matching graphs with equations
- Assignment: P. 436-437 (1-31, 38-39)

Linear versus quadratic

Mr. Wiggins gives his daughter Celia two choices of payment for raking leaves:

Two dollars for each bag of leaves filled,
She will be paid for the number of bags of leaves she rakes as follows: two cents for filling one bag, four cents for filling two bags, eight cents for filling three bags, and so on, with the amount doubling for each additional bag filled.

If Celia rakes enough to five bags of leaves, should she opt for payment method 1 or 2? What if she fills ten bags of leaves?
How many bags of leaves would Celia have to fill before method 2 pays more than method 1?

Linear versus quadratic task

Linear versus Quadratic task 1-2

[/expand]

x = h