Concept 1 – Introduction to Probability

Week 5 – Experimental or Theoretical Probability

Portion Web Task Cards Portion Web Practice
Accordion Sample Description

Write a short statement or sentence for each of the following:

  • Think of something that certain or guaranteed to happen
  • Think of something that is impossible, or could not happen
  • Now, think of something in between
Probability Scale
Mike wants to win a giant stuffed animal at the carnival.  He decided to play the “Go Fish” game, which has three prizes: a giant stuffed animal, a smaller stuffed animal, and a plastic kazoo. The game is set up with a tank containing 1 green fish, 3 blue fish, and 6 yellow fish.  To play, Mike must go fishing.  The game is set up so that every time a player goes fishing, he or she will catch a fish. To win the giant stuffed animal, Mike needs to catch a green fish.
  1. Create a drawing of the game by creating a bag with tiles matching the fish colors.
  2. If all of the fish in the tank are green, how would you describe the probability of Mike’s winning a giant stuffed animal?
  3. The way the tank is set up (with 1 green, 3 blue, and 6 yellow fish), what are the chances that Mike will catch a black fish?
  4. What percent of the time would you expect Mike to catch a green fish and win the giant stuffed animal?  How can you explain this thinking to the class?
  5. What is the probability that Mike will catch a blue fish?  A yellow fish?  Write each of these probabilities as a fraction and a percent.
1-52.  In the game described in problem 1-51, you could expect Mike to win a giant stuffed animal 10% of the time.  A percentage is one way to express the probability that a specific event will happen.  You might also have said you expected Mike to win 1 out of every 10 attempts.  So the probability that Mike will win is , because the 1 represents the number of desired outcomes (green fish that Mike can catch) and the 10 represents the number of possible outcomes (all the fish that Mike could catch)
Go Fish - WB

1-63. THE MYSTERY SPINNER

Your teacher has a hidden spinner.  Your challenge is to perform an experiment that will allow you to predict what the spinner looks like without ever seeing it.

Your Task: Your teacher will spin the spinner and announce each result.  When you think you know what it looks like, draw a diagram of the spinner.

  1. Based on your data, how can you describe the likelihood of landing on each part of the spinner?  How does the spinner that your team drew represent these likelihoods?  
  2. Use your data to write the probability of each of the following results as a fraction, a decimal, and a percent.
    1. The spinner lands on purple.
    2. The spinner lands on green or orange.
  3. If your teacher were to spin the spinner 15 more times, how might this change your answers for part (b)?
  4. Do you know for sure that the spinner you drew looks exactly like your teacher’s?  Are you certain that the portions that you drew for each color are the same size as the portions on your teacher’s spinner?  Why or why not?
Mystery Spinner Revealed!

Assignment: 1.2.2 Homework

Concept Summary

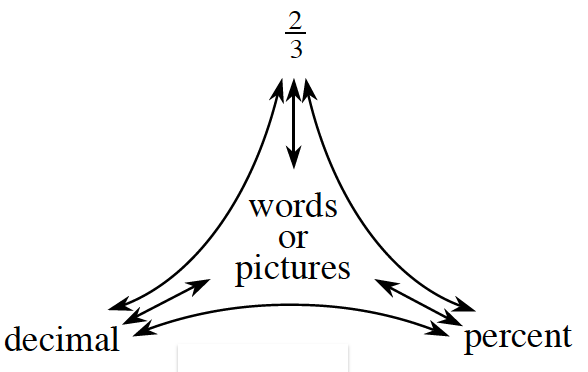
In the game described in problem 1-51, you could expect Mike to win a giant stuffed animal 10% of the time.  A percentage is one way to express the probability that a specific event will happen.  You might also have said you expected Mike to win 1 out of every 10 attempts.  So the probability that Mike will win is 1/10, because the 1 represents the number of desired outcomes (green fish that Mike can catch) and the 10 represents the number of possible outcomes (all the fish that Mike could catch).

Probabilities such as these are called theoretical probabilities because they are calculated mathematically based on what is expected. In other words, it is what we think or predict would happen, given what we see or are given.

Theoretical Probability is a calculated probability based on the possible outcomes when they all have the same chance of occurring.

Theoretical Probability = 

pic

 

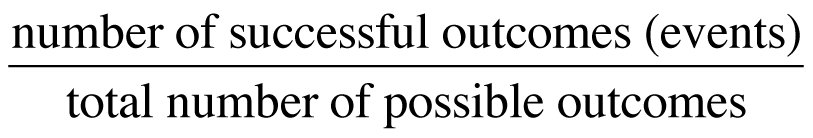
Experimental Probability, however is the ratio of number of successful events over the number of trials.

Week 6 – Compound Probability

1-119. Thomas helps around the house by doing one chore after school.  Each day, Thomas and his aunt use the spinner at right to decide which chore he will do. Here is what Thomas knows: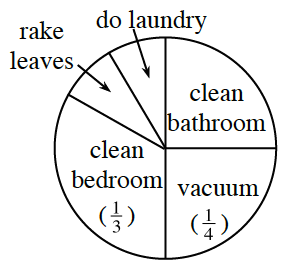pic

  • The sections on the spinner for “rake leaves” and “do laundry” are the same size.
  • The sections for “clean bathroom” and “vacuum” are equal in size and together make up half the spinner.
  1. What is the probability that Thomas will spin “do laundry”?
  2. Thomas hates to clean the bathroom.  When he spins the spinner, what is the probability that it will not point to “clean bathroom”?  Explain how you found your answer.

Thomas’s aunt hopes that he will either spin “clean bedroom” or “rake leaves” today.

  1. What is P(clean bedroom)?  What is P(rake leaves)?

Spinning either chore in part (a) would make Thomas’s aunt happy. 

  1. What is the probability that he will spin either one of the chores?
  2. How can you write the two outcomes as a single probability?
  3.  
Roberto was playing a game that required spinning a spinner. On his first ten spins, he landed on four different spaces. He landed on: Lose a Turn one time Move Forward One Space four times Move Forward Two Spaces three times Move Back One Space two times
  1. Based on this data, what is the probability that Roberto will spin Move Forward Two Spaces on his next spin? Why?
  2. Based on this data, what is the probability he will NOT land on Move Back One Space on his next spin? Why?
  3. Based on this data, what do you think this spinner looks like? Explain your thinking with words.
Game spinner - WB Pick a tile
Lindsay has a paper bag full of Fruiti Tutti Chews in three different fruit flavors.  She says, “If you reach into the bag, you have a pic chance of pulling out a Killer Kiwi.  There is a pic chance that you will get Crazy Coconut.”  
  1. If you reach into the bag, what is P(coconut or kiwi)?
  2. Does there have to be another flavor in the bag?  How can you tell?  If so, assuming that there is only one other flavor, what is the probability of getting that flavor?
  3. How many candies might Lindsay have in the bag?  Is there more than one possibility?  Assume that all candies in the bag are whole candies.
Fruity Tutti Chews - WB
Candy Probability

We have a bag containing a set of colored blocks or counters. The bag contains 1 yellow, 2 red, 4 green, and 5 blue blocks.

  1. Are we working with Experimental or Theoretical probability?
  2. Look at the blocks in your bag.  If you were to reach into the bag and select one block without looking, what is the likelihood that it would be:
  • Red?
  • Green?
  • Blue?
  • Orange?

If you were to select one block from the bag 12 times, replacing the block you drew between each selection, how many of those times would you expect to have selected a blue block?  What if you drew 24 times?  Discuss both situations with your team and explain your answers.

  1. Do you think the larger sample space will change the likelihood of drawing blocks of different colors?
  2. Do you think the probabilities would change if you combined three bags?  Why or why not?
  3. What change do you think you could make in order to increase the chances of choosing a blue block?  Explain your reasoning.

Assignment: 1.2.3 Homework

Week 7 – Additional Probability

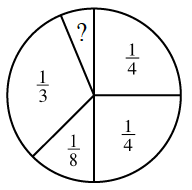
James is playing a game, but the spinner is incomplete.  Each section of the spinner is labeled with the probability of spinning it.  What fraction is missing? James está jugando, pero la ruleta está incompleta. Cada sección de la ruleta está etiquetada con la probabilidad de girarla. ?Que fraccion falta?
picCharles found a spinner his teacher was making.  He knew that if he put his problem-solving skills to use, he would be able to figure out the missing piece and finish the spinner for his teacher.

James' spinner - WB
1.2.8-homework
Pick a Tile Gina has a bag containing Red, Green, Blue, Yellow, and White tiles. If someone picks a tile without looking: • The probability of picking a Red tile from the bag is one half. • The probability of picking a Green tile is half the probability of picking a Red tile. • Blue, Yellow, and White tiles have an equal probability of being picked. Use this information to complete the table.
Pick a tile
1-121. Ms. Woodbury lets her students borrow pens and pencils on days when they have a quiz. She has a paper bag containing hundreds of wooden pencils, mechanical pencils, and blue pens. Stuart forgot his pencil, and it is quiz day! Ms. Woodbury tells him:
  • One out of every three students who reaches into the bag pulls out a wooden pencil.
  • Two out of every five students pull out a mechanical pencil. The rest of the students pull out a blue pen.
  • If Stuart reaches into the bag without looking, is it more likely that he will choose a wooden pencil or a mechanical pencil?
  • How can you describe the probability that Stuart will pull out some kind of pencil—either a wooden pencil or a mechanical pencil—by using the probabilities that you already know?
Pencils for class - WB
Pick a tile 2
1-132. Lyle asked for a challenge problem, and his teacher gave him this one:
There is a 2/7 chance of drawing a red marble out of a bag of marbles. If the probability of drawing a red or a blue marble is 2/3, what is the probability of drawing a blue marble?
When Lyle’s teammates saw the challenge he was working on, they each had a different idea for how he should start.
Mayra suggested that he start by rewriting 2/7 and 2/3 so that they have a common denominator.
Kenessa disagreed. “You want to set up a subtraction problem,” she said. She wrote the expression 2/3 − 2/7 to show the number Lyle needs to find.
Darren had a different idea. “The probability that you would draw either red or blue is the same as the probability of drawing red added to the probability of drawing blue,” he said. He wrote this expression: 2/7 + ? = 2/3
Which way would you suggest Lyle start working to find P(blue)? Discuss your ideas with your study team.
Write a clear explanation of which method you recommend and why. Include your ideas about whether the other strategies will solve the problem and why you did not choose them. What is the probability of drawing a blue marble? Explain your reasoning