Week 21 – Probability Games
- What is the probability that Travis will win?
- What is the probability that Xavier will win?
- Is this a fair game? Why or why not?
If there is an equal chance for each player to win a game, then it is considered to be a fair game. If it is not equally likely for each player to win, a game is considered to be unfair.
5-23. PICK A CARD, ANY CARD What is the probability of picking the following cards from the deck? Write your response as a fraction, as a decimal, and as a percent.
a. P(black)?
b. P(club)?
c. If you drew a card from the deck and then replaced it, and if you repeated this 100 times, about how many times would you expect to draw a face card (king, queen, or jack)?
5-24. Sometimes it is easier to figure out the probability that something will not happen than the probability that it will happen. This is called finding the probability of the complement.
Everything in the sample space that is not in the event is in the complement.
a. What is the probability you do not get a club, written P(not club)?
b. What is P(not face card)?
c. What would happen to the probability of getting an ace on a second draw if you draw an ace on the first draw and do not return it to the deck?
Xavier and Travis Card Game - WB
Assignment: 5.2.1 Homework
- If you buy a scratch-off ticket, is it more likely that you will win a free raffle ticket or a cash prize? Explain your answer.
- What is the probability that you will win something (either a free raffle entry or a cash prize)?
- What is the probability that you will win nothing at all? To justify your thinking, write an expression to find the complement of winning something.
- One of the new advertisements states that if you reach into any bag of Fruiti Tutti Chews, you have a probability of pulling out a Killer Kiwi candy. Another advertisement says that of each bag is Ridiculous Raspberry. Are the advertisements telling the truth?
- Alicia learns that when she opens a new bag of candy, she has a chance of pulling out a piece of Ridiculous Raspberry and a chance of pulling out a piece of Killer Kiwi. Could she have a chance of pulling out a piece of Perfect Peach?
- When the company introduces the new flavor, it plans to make Perfect Peach of the candy in each bag. If there is an equal amount of the remaining three flavors, what is the probability that the first piece you pull out of the bag will be Crazy Coconut?
- Make a list of all the possible combinations. Is there a better way to organize this list?
- How many possible outfits can she make?
- What is the probability that she will wear both a pajama pants and a cropped top shirt?
- What is the probability that she will not wear the cargos?
- If she were to only wear her hoodie because it is raining, how many possible outfit combinations can she make?
Rona's Clothes - WB
5-69. Represent all of the possible outcomes using a list, probability table, or probability tree. Then find the indicated probability in each situation below.
- You flip a coin three times in a row and get
 heads exactly twice.
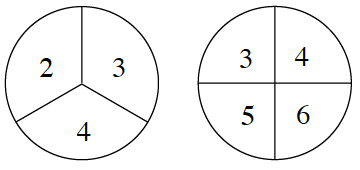
heads exactly twice. - You spin the two spinners at right and exactly one spinner lands on 4.
- At the car rental agency, you will be given either a truck or a sedan. Each model comes in four colors: green, black, white, or tan. If there is one vehicle of each color for each model available, what is the probability you will get a green truck?

5-34. RANDOM NUMBER GENERATOR
Imagine a random number generator that produces numbers from 1 to 20. In each game below, if the stated outcome happens, Player X wins. If it does not, then Player Y wins.
Explore using the 5-34 Student eTool (CPM) to randomly generate a number from 1 to 20.
| Game 1: A prime number = Player X wins |
| Game 2: An even number = Player X wins |
| Game 3: A number not divisible by three = Player X wins |
a. In each case, what is the theoretical probability that Player X wins? That Player Y wins? Decide whether each game above is fair.
b. In which of the three games is Player X most likely to win? Why?
c. In Game 1, the prime number game, if you play 40 times, how many times would you expect Player X to win? What if you played 50 times?
d. Obtain a random number generator from your teacher and set it up to generate integers from 1 to 20. Play the prime number game (Game 1) ten times with a partner. Start by deciding who will be Player X and who will be Player Y. Record who wins each time you play.
e. How did the experimental and theoretical probabilities of Player X’s winning from part (a) and part (d) compare?
5-35. Janelle is going to babysit her nephew all day five times this summer. She had the idea that one way to entertain him is to walk to McBurger’s for a Kids Meal for lunch each time. The Kids Meal comes packed randomly with one of three possible action figures. Janelle would like to know the probability that they get all three figures in five trips.
Explore using the 5-35 Student eTool (CPM) to generate random numbers to simulate the problem below.
a. Call the action figures #1, #2, and #3. Use the random number generator to simulate five trips to McBurger’s. Did you get all three action figures?
b. Simulate another five trips to McBurger’s. Did you get all three action figures this time? Do the simulation at least 20 times (that is, 20 sets of 5 random numbers), keeping track of how many times you got all three action figures in five tries, and how many times you did not.
c. Use your results to estimate the probability of getting all three action figures in 5 trips. Should Janelle be worried?
d. How could Janelle get an even more accurate estimation of the probability?
5-36. Janelle’s aunt and uncle have three children, two of whom are girls. Assuming that girl children and boy children are equally likely, Janelle thought that the chance of having two or more girls out of 3 children must be 50%. Janelle’s brother thought the chance of having so many girls had to be less than 50%.
Explore using the 5-36 Student eTool (CPM) to randomly generate numbers to indicate the number of girls and boys in a family with three children.
a. What do you think? Make a conjecture about the probability of having two or three girls in a family of three siblings.
b. Do a computer simulation with the random number generator to estimate the probability of having two or three girls in a family of three siblings. Use a 1 to represent a girl and a 0 to represent a boy and simulate a family of three children. Do enough trials to get a good estimate.
Additional Challenge 5-37. Sophia and her brother are trying to create a fair game in which you roll two number cubes. They cannot agree on the probability that the numbers on both number cubes will be even, so they decide to design a simulation.
Explore using the 5-37 Student eTool (CPM) to simulate the problem below.
a. Make a conjecture. What is the probability both dice are even?
b. Design a simulation with a random number generator. How many random numbers do you need? In what interval should the numbers be? How many times will you do the simulation?
c. Set up and run the simulation that you designed with the random number generator and estimate the probability. How does it compare with your conjecture from part (a)?
Assignment: 5.2.2 Homework
[/expand]
[expand title=”Week 20 – Compound Probability”]
5-43. In Chapter 1, you met Chris and her older sister, Rachel, who made a system for determining which one of them washes the dishes each night. Chris has been washing the dishes much more than she feels is her fair share, so she has come up with a new system. She has proposed to Rachel that they get two coins, and each day she and Rachel will take a coin and flip their coins at the same time. If the coins match, Chris washes the dishes; if they do not match, Rachel washes the dishes. Explore using CPM Probability eTool (CPM).
Rachel thinks that this is a good idea and that her little sister is very silly! She thinks to herself, “Since there are two ways to match the coins, Heads-and-Heads or Tails-and-Tails, and only one non-match, Heads-and-Tails, then Chris will STILL wash the dishes more often. Ha!”
a. Do you agree with Rachel? Why or why not?
b. Does it matter if they flip the coins at the same time? That is, does the result of one coin flip depend on the other coin flip?
c. What are all of the possible outcomes when the girls flip their coins? Organize the possibilities. Use the word “and” when you are talking about both one thing and another occurring.
d. Look at your list from part (c). Imagine that the coins are a penny and a nickel instead of two of the same coin. Does your list include both the possibilities of getting a heads on the penny and tails on the nickel and vice versa? If not, be sure to add them to your list.
e. Is Rachel right? Does this method give her an advantage, or is this a fair game? What is the theoretical probability for each girl’s washing the dishes?
5-44. ROCK-PAPER-SCISSORS
Read the rules for the Rock-Paper-Scissors game below. Is this a fair game? Discuss this question with your team.
a. While both players are making their choice at the same time, this game has two events in every turn. What are the two events?
b. If you and a partner are playing this game and you both “go” at the same time, does your choice affect your partner’s choice? Explain.
c. Are the two events in this game dependent (where the outcome of one event affects the outcome of the other event) or independent (where the outcome of one event does not affect the outcome of the other event)? Explain your reasoning.
d. Work with your team to determine all of the possible outcomes of a game of rock-paper-scissors, played by two people (call them Person A and Person B). Be sure to include the word “and.” For each outcome, indicate which player wins or if there is a tie. Be prepared to share your strategies for finding the outcomes with the class.
5-45. Is Rock-Paper-Scissors a fair game? How can you tell?
5-46. Imagine that two people, Player A and Player B, were to play rock-paper-scissors 12 times.
a. How many times would you expect Player A to win? Player B to win?
b. Now play rock-paper-scissors 12 times with a partner. Record how many times each player wins and how many times the game results in a tie.
c. How does the experimental probability for the 12 games that you played compare to the theoretical probability that each of you will win? Do you expect them to be the same or different? Why?
5-47. Identify the situations below as either dependent or independent events.
a. Flipping a “heads” on a quarter and then flipping another “heads.”
b. Choosing a jack from a standard deck of cards, not putting it back in the deck, and then choosing a king.
c. Picking a blue marble from a bag of marbles, putting it back, and then picking a blue marble again.
d. Rolling a 6 on a number cube three times in a row.
5-48. LEARNING LOG
In your Learning Log, make an entry that summarizes your understanding of independent and dependent events. Explain how to decide if two events are independent or dependent when looking at their likelihood. Give a few examples to support your thinking. Title your notes “Independent and Dependent Events” and include today’s date.
Assignment: 5.2.3 Homework
Probability tables: a new strategy for organizing all of the possibilities in a complicated game.
5-54. TEN Os
In this game, you will create a strategy to play a board game based on your predictions of likely outcomes. You will place ten O’s on a number line. Then your teacher will roll two number cubes and add the resulting numbers. As your teacher rolls the number cubes and calls out each sum, you will cross out an O over the number called. The goal of the game is to be the first person to cross out all ten of your O’s. Create number cubes using the 5-54 Ten 0’s Game (CPM).
Talk with your team about the possible outcomes of this game. Then draw a number line like the one below on your own paper. Place a total of ten O’s on your number line. Each O should be placed above a number. You should distribute them based on what results you think your teacher will get. More than one O can be placed above a number.
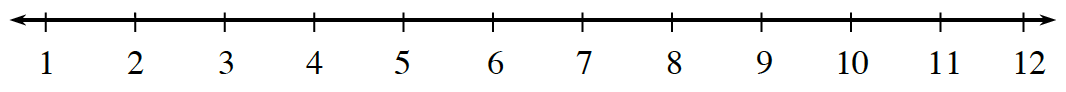
Follow your teacher’s instructions to play the game.
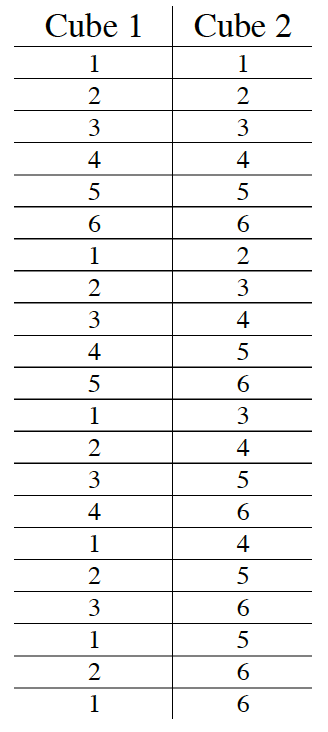 5-55. Gerald’s strategy for the Ten O’s game was to place an O on each number from 1 to 10. He was frustrated that his strategy of placing his ten O’s was not working, so he decided to analyze the game.
5-55. Gerald’s strategy for the Ten O’s game was to place an O on each number from 1 to 10. He was frustrated that his strategy of placing his ten O’s was not working, so he decided to analyze the game.
Gerald began by trying to create a table to list all of the possible combinations of rolls. He made the table at right.
Did he list them all? If so, how can you be sure that they are all there? If not, give examples of a few that he has missed.
5-56. Gerald decided that this method was taking too long, that it was too confusing, and that he made too many mistakes. Even if he listed all of the combinations correctly, he still had to find the sums and then find the theoretical probabilities for each one. Inspired by multiplication tables, he decided to try to make sense of the problem by organizing the possibilities in a probability table like the one shown below right.
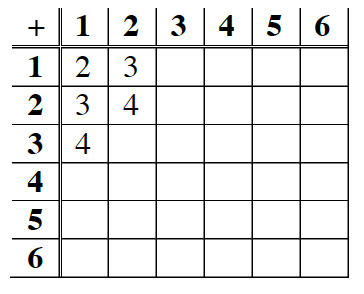 a. How does Gerald’s table represent the two events in this situation? What should go in each of the empty cells? Discuss this with your team and then complete Gerald’s table on your own paper or explore using the 5-56 Student eTool (CPM).
a. How does Gerald’s table represent the two events in this situation? What should go in each of the empty cells? Discuss this with your team and then complete Gerald’s table on your own paper or explore using the 5-56 Student eTool (CPM).
b. How many total possible number combinations are there for rolling the two cubes? Is each combination listed equally likely? That is, is the probability of getting two 1’s the same as that of getting two 2’s or a 3 and a 1?
c. How many ways are there to get each sum? Are there any numbers on the game board that are not possible to achieve?
d. What is the theoretical probability for getting each sum listed on the Ten O’s game board?
e. Now work with your team to determine a better strategy for Gerald to place his ten O’s on the game board that you think will help him to win this game. Explain your strategy and your reasoning.
5-57. Gloria and Jenny each have only one O left on their game board. Gloria’s O is at 6, and Jenny’s is at 8. Which student is more likely to win on the next roll? Explain.
5-58. Now go back and analyze the game of rock‑paper-scissors using a probability table to determine the possible outcomes.
a. Make a probability table and use it to find the probability of Player A’s winning and the probability of Player B’s winning. Did you get the same answers as before?
b. Do the probabilities for Player A’s winning and Player B’s winning add up to 1 (or 100%)? If not, why not?
5-59. Imagine that you have a bag with a red block, a blue block, a green block, and a yellow block inside. You plan to make two draws from the bag, replacing the block after each draw.
- Are these two events (the two draws of a block) independent or dependent? Does it matter if you replace the block each time? Why or why not?
- Find the probability of getting a red block and a blue block. (Either color can come first.) Be ready to share your method of organizing the possible outcomes.
Assignment: 5.2.4 Homework
[/expand]
[expand title=”Week 21 – Probability Trees”]
 5-65. THE DOUBLE SPIN
5-65. THE DOUBLE SPIN
A giant wheel is divided into 5 equal sections labeled –2, –1, 0, 1, and 3. At the Double Spin, players spin the wheel shown at right two times. The sum of their spins determines whether they win. Explore using 5-65 Spinner eTool (CPM).
Work with your team to determine probabilities of different outcomes by answering the questions below.
Make a list of the possible sums you could get.
a. Which sum do you think will be the most probable?
b. Create a probability table that shows all possible outcomes for the two spins.
c. If Tabitha could choose the winning sum for the Double Spin game, what sum would you advise her to choose? What is the probability of her getting that sum with two spins?
5-66. Scott’s job at Crazy Creations Ice Cream Shop is to design new ice cream flavors. The company has just received some new ingredients and Scott wants to be sure to try all of the possible combinations. He needs to choose one item from each category to create the new flavor.
a. Without talking with your teammates, list three different combinations Scott could try. Make sure you use the word “and.” Then share your combinations with your study team. How many different combinations did you find? Do you think you found all of the possibilities?
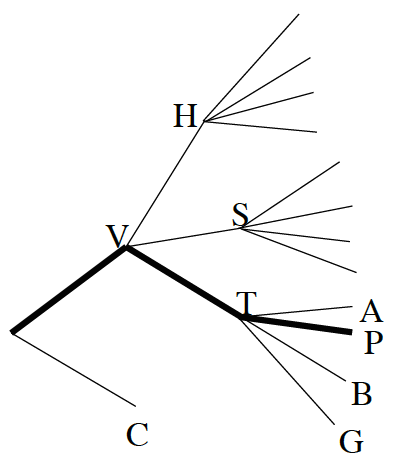 Creating a list of all of the possibilities would take time and require a lot of writing the same words over and over. Because there are more than two options, a probability table is also challenging. An alternative is creating a probability tree to show the different combinations. A probability tree, like the one started at right and on the Lesson 5.2.5 Resource Page, shows the different possibilities branching off each other. In this case, the two segments on the left show the base flavors. Each different mix-in choice branches off of the base flavor, and each fruit swirl branches off each mix-in choice. The first letter of each choice is used to label this diagram.The bold line in the diagram shows the combination vanilla, toffee bits and plum swirl. Complete the probability tree to show all of the possible combinations.
Creating a list of all of the possibilities would take time and require a lot of writing the same words over and over. Because there are more than two options, a probability table is also challenging. An alternative is creating a probability tree to show the different combinations. A probability tree, like the one started at right and on the Lesson 5.2.5 Resource Page, shows the different possibilities branching off each other. In this case, the two segments on the left show the base flavors. Each different mix-in choice branches off of the base flavor, and each fruit swirl branches off each mix-in choice. The first letter of each choice is used to label this diagram.The bold line in the diagram shows the combination vanilla, toffee bits and plum swirl. Complete the probability tree to show all of the possible combinations.- How many different flavor combinations are possible? Where do you look on the diagram to count the number of complete combinations?
- Use your probability tree to help you find the probability that Scott’s final combination will include plum swirl.
- What is the probability that his final combination will include hazelnuts
5-67. Scott’s sister loves hazelnuts and Scott’s little brother loves grape.
- Recall that events are favorable outcomes. List all of the outcomes in Scott’s sister’s event. List all the outcomes in Scott’s little brother’s event.
- Two events are mutually exclusive if they have no outcomes in common. Do Scott’s sister and little brother have mutually exclusive events?
- What would two mutually exclusive events in the Crazy Creations Ice-Cream Shop be?
5-68. In a power outage, Rona has to reach into her closet in the dark to get dressed. She is going to find one shirt and one pair of pants. She has three different pairs of pants hanging there: one black, one brown, and one plaid. She also has two different shirts: one white and one polka dot.
- Draw a probability tree to organize the different outfit combinations Rona might choose.
- What is the probability that she will wear both a polka dot shirt and plaid pants?
- What is the probability that she will not wear the black pants?
- For what kinds of problems can you also make a probability table? If it is possible, make a probability table for Rona’s outfits. Which way of representing the outcomes do you like better?
- Are the events polka dot and plaid mutually exclusive? Explain. .
- Are the events polka dot and white mutually exclusive? Explain.
5-69. Represent all of the possible outcomes using a list, probability table, or probability tree. Then find the indicated probability in each situation below.
 You flip a coin three times in a row and get heads exactly twice.
You flip a coin three times in a row and get heads exactly twice.- You spin the two spinners at right and exactly one spinner lands on 4.
- At the car rental agency, you will be given either a truck or a sedan. Each model comes in four colors: green, black, white, or tan. If there is one vehicle of each color for each model available, what is the probability you will get a green truck?
Assignment: 5.2.5 Homework

5-76. Nina is buying a new pet fish. At the pet store, the fish tank has an equal number of two kinds of fish: tetras and guppies. Each kind of fish comes in four different colors: yellow, orange, blue, and silver. There are an equal number of each color of fish in the tank.
a. If Nina scoops out a fish at random, what is the probability that she will scoop out a silver tetra? Show how you decided.
b. Nina set up the table below, to organize the different possible outcomes. She represented the kind of fish on one side of her table and the color possibilities on the other. What do the fractions inside her table represent?

c. As Nina looked at her work, she noticed that her table looked a lot like a rectangle with the area divided into parts. “Could that help me calculate the probabilities?” she wondered. She used the length and width of the silver tetra section to set up this equation: ![]() .How does this equation relate to the length, width, and area of this section of the rectangle? Does this match the probability you found in part (a)?
.How does this equation relate to the length, width, and area of this section of the rectangle? Does this match the probability you found in part (a)?
d. What is the area of the complete large rectangle?
5-77. TESTING THE AREA MODEL
Nina decided to see if thinking about finding area would help find other probabilities. She put three cubes in a bag: two blue cubes and one yellow cube. 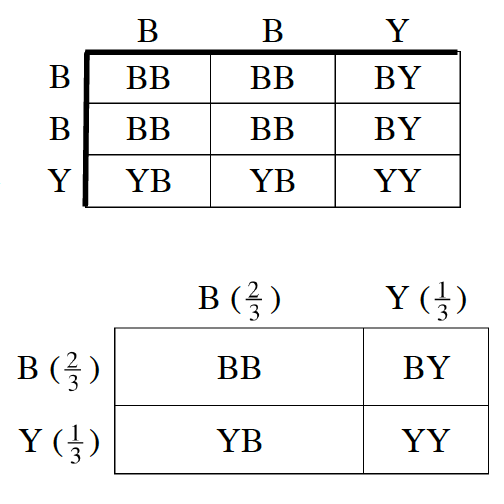 She pulled one cube out, put it back in the bag, and then drew another.
She pulled one cube out, put it back in the bag, and then drew another.
a. Use a systematic list or a probability tree to organize the possible color combinations she could draw. How many are there? What is P(blue and blue)?
b. This time, Nina made the table at right. Based on the table, what is the probability of drawing two blue blocks? Is this the same probability you found in part (a)?
c. Looking at her work, Edwin said, “I think I can simplify this diagram.” His rectangle is shown at right. What is the area of the section representing blue and blue? Does this match the probability that Nina found?
5-78. The pet store sells a lot of pet food. On a slow day at the pet store, three people buy cat food, two people buy dog food, and one person buys food for a pet snake. If half of the customers pay with cash and half pay with credit card, what is the probability that a customer buying pet food will buy dog food with cash? Set up an area model like Edwin’s in part (c) of problem 5‑77 to help you find the probability.
5-79. SPINNING ODDS AND EVENS — PART 1
Your team is going to play against your teacher in a game with two hidden spinners. Spinner A has the numbers 2, 3, and 4 on it. Spinner B has the numbers 6, 7, and 8 on it.
The rules are:
- Spin each spinner.
- Add the results.
- If the sum is even, one team gets a point. If the sum is odd, the other team gets a point.
- The first team to earn 10 points wins.
a. Should you choose the odd or even numbers in order to win? Discuss the choices with your team and decide which side to take. Be prepared to justify your choice with mathematics.
b. Play the game at least three times with your teacher. Your teacher will spin the spinners and announce the results. Record the results of each spin and their sum. Is the result odd or even most often? Does this match with your prediction?
c. Make a probability table and determine the theoretical probability for this game.
5-80. SPINNING ODDS AND EVENS — PART 2
Now that you have played the game several times, obtain a Lesson 5.2.6 Resource Page from your teacher and take a close look at the hidden spinners.
a. Are the spinners different from what you expected? How? Be as specific as you can. Do you still think you made the correct choice of odd or even numbers?
b. What assumption about the spinners did you make in part (c) of problem 5‑79?
c. What is the probability of spinning each outcome on Spinner A? On Spinner B?
5-81. 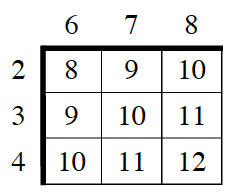 Raul had imagined that the spinners were divided into equal parts before he saw them. He created the probability table at right to organize the outcomes. “I thought there would be a
Raul had imagined that the spinners were divided into equal parts before he saw them. He created the probability table at right to organize the outcomes. “I thought there would be a ![]() chance of spinning a 3 on Spinner A. But now that I see the spinners, I know that is not true. I need to make a new rectangle in order to find the probability.”
chance of spinning a 3 on Spinner A. But now that I see the spinners, I know that is not true. I need to make a new rectangle in order to find the probability.”
a. Create a new rectangle. Label the top row and left column with the numbers on each spinner and their probabilities.
b. Write a multiplication problem to show the probability of spinning a 3 and a 7. Calculate P(3 and 7).
c. Complete the table to show each possible sum and its probability.
d. What is the probability of spinning an odd sum? What is the probability of spinning an even sum?
e. Did you make the right choice of an odd or even number in problem 5-80? Explain your reasoning.
5-82. Additional Challenge: Elliot loves music, especially listening to his music player on shuffle. He has songs stored in four categories: country, blues, rock, and classical. Two fifths of his songs are country songs, one sixth of his songs are classical, one third are blues, and the rest are rock.
a. What is the likelihood that the first two songs will be a country song and then a classical?
b. What is the likelihood that either a country song or a classical song will come up first?
Assignment: 5.2.6 Homework
[/expand]