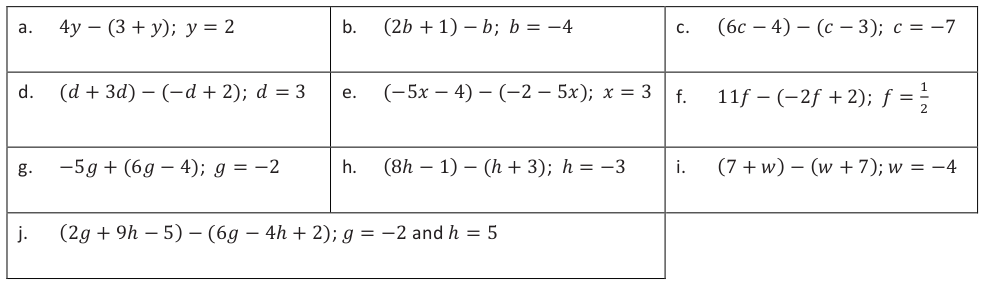Introduction to Expressions
[expand title=”Numerical and Variable Expressions”]
In class (remainder is homework)
Generating numerical expressions given a target numerical value.
- ML.7.EE.1-3
Class Challenge Activity: Using the numbers 1, 2, 3, 4, and 5, make the target numerical values 1 -30
- PH 2-1 (Properties of numbers and Mental Math)
The distributive property – Mental Math
- How can we use the distributive property to make multiplication easier to do in our head? (You may already be doing this!)?
- The distributive property is also one of the simplest theorems to prove.
Example 1.
| 3 × 24 | = | 3 × 20 + 3 × 4 |
| = | 60 + 12 | |
| = | 72. | |
We expanded 24 into 20 + 4, and then “distributed” 3 to each one.
Look:
| 3 × 24 | = | 24 + 24 + 24 |
| = | 20 + 4 + 20 + 4 + 20 + 4 | |
| = | 20 + 20 + 20 + 4 + 4 + 4 | |
| = | 3 × 20 + 3 × 4. | |
The repeated addition of 24 is equal to the repeated addition of 20, plus the repeated addition of 4.
Example 2:
Multiply 5 × 37 mentally.
Example 3:
Multiply 800 × 460 mentally.
Assignment: PH 2-2
[/expand]
Working with expanded form to uncover how to simplify expressions
[expand title=”Expanded form”]
Opening Exercise: Triangle or quadrilateral?
- Draw a triangle or a square – Keep it secret!
a. What if we add them all up?
b. How many triangles are there? How many squares?
c. Write and expression representing the number of triangles and squares at your table group.
d. Write and expression representing the total number of triangles and squares in the room.
e. How do parts a and d relate?
Making a connection to variable expressions
- Write down an X or a Y – Keep it secret!
a. Can we write expressions to represent the number of X’s and Y’s at each table?
b. Simplify the expression to find the total number of X’s and Y’s in the class.
c. Explain, in your own words how to simplify variable expressions.
[/expand]
Use Properties of operations to generate equivalent expressions (7.EE.1)
[expand title=”Generating equivalent expressions”]
Example 1: Any Order, Any Grouping Property with Addition
a. Rewrite and
by combining like terms.
Write the original expressions and expand each term using addition. What are the new expressions equivalent to?
b. Find the sum of and
c. Find the sum of and
Example 2: Any Order, Any Grouping with Multiplication
Find the product of and
.
Example 3: Any Order, Any Grouping in Expressions with Addition and Multiplication
a. 3(2x)
b. 4y(5)
c. 4 ∙ 2 ∙z
d. 3(2x) + 4y(5)
e. 3(2x) + 4y(5) + 4 ∙ 2 ∙ z
f. Alexander says that 3x + 4y is equivalent to (3)(4) + xy because of any order, any grouping. Is he correct? Why or why not?
Exit Ticket
1. Write an equivalent expression to 2x + 3 + 5x + 6 by combining like terms.
2. Find the sum of (8a + 2b − 4) and (3b − 5).
3. Simplify 4(2a) + 7(−4b) + (3 ∙ c ∙ 5).
Problem Set
For problems 1–9, write equivalent expressions by combining like terms. Verify the equivalence of your expression and
the given expression by evaluating each for the given values: a = 2, b = 5, and c = −3.
[ezcol_2fifth]
1. 3a + 5a
2. 8b − 4b
3. 5c + 4c + c
4. 3a + 6 + 5
[/ezcol_2fifth]
[ezcol_3fifth_end]
5. 8b + 8 − 4b
6. 5c − 4c + c
7. 3a + 6 + 5a − 2
8. 8b + 8 − 4b − 3
9. 5c − 4c + c − 3c
[/ezcol_3fifth_end]
Use any order, any grouping to write equivalent expressions by combining like terms. Then verify the equivalence of
your expression to the given expression by evaluating for the value(s) given in each problem.
[ezcol_2fifth]
10. 3(6a); for a = 3
11. 5d(4); for d = −2
12. (5r)(−2); for r = −3
[/ezcol_2fifth][ezcol_3fifth_end]
13. 3b(8) + (−2)(7c); for b = 2, c = 3
14. −4(3s) + 2(−t); for s = , t = −3
15. 9(4p) − 2(3q) + p; for p = −1, q = 4
16. 7(4g) + 3(5h) + 2(−3g); g = , h = 2
[/ezcol_3fifth_end]
The problems below are follow-up questions to Example 1b from Classwork: Find the sum of 2x + 1 and 5x.
17. Jack got the expression 7x + 1, then wrote his answer as 1 + 7x. Is his answer an equivalent expression? How do you know?
18. Jill also got the expression 7x + 1, then wrote her answer as 1x + 7. Is her expression an equivalent expression? How do you know?
[/expand]
[expand title=”Combining expressions with addition and subtraction”]
Example 1: Subtracting Expressions
a. Subtract: (40 + 9) − (30 + 2).
b. Subtract: (3x + 5y − 4) − (4x + 11).
Example 2: Combining Expressions Vertically
a. Find the sum by aligning the expressions vertically.
(5a + 3b − 6c) + (2a − 4b + 13c)
b. Find the difference by aligning the expressions vertically.
(2x + 3y − 4) − (5x + 2)
Example 3: Using Expressions to Solve Problems
A stick is x meters long. A string is 4 times as long as the stick.
a. Express the length of the string in terms of x.
b. If the total length of the string and the stick is 15 meters long, how long is the string?
Example 4: Expressions from Word Problems
It costs Margo a processing fee of $3 to rent a storage unit, plus $17 per month to keep her belongings in the unit. Her friend Carissa wants to store a box of her belongings in Margo’s storage unit and tells her that she will pay her $1 toward the processing fee and $3 for every month that she keeps the box in storage. Write an expression in standard form that represents how much Margo will have to pay for the storage unit if Carissa contributes. Then, determine how much Margo will pay if she uses the storage unit for 6 months.
Problem Set
7.3.1.ProblemSet.CombiningSubtraction
1. Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating
each expression using x = 5.
j. In problems (a)–(d) above, what effect does addition have on the terms in parentheses when you removed the
parentheses?
k. In problems (e)–(i), what effect does subtraction have on the terms in parentheses when you removed the
parentheses?
2. Write each expression in standard form. Verify that your expression is equivalent to the one given by evaluating
each expression for the given value of the variable.
5.Write each word problem in standard form as an expression.
- Find the sum of −3x and 8x.
- Find the sum of – 7g and 4g + 2.
- Find the difference when 6h is subtracted from 2h − 4.
- Find the difference when −3n − 7 is subtracted from n + 4.
- Find the result when 13v + 2 is subtracted from 11 + 5v.
- Find the result when −18m − 4 is added to 4m − 14.
- What is the result when −2x + 9 is taken away from −7x + 2?
6. Marty and Stewart are stuffing envelopes with index cards. They are putting x index cards in each envelope. When they are finished, Marty has 15 envelopes and 4 extra index cards, and Stewart has 12 envelopes and 6 extra index cards. Write an expression in standard form that represents the number of index cards the boys started with. Explain what your expression means.
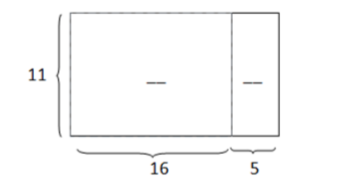
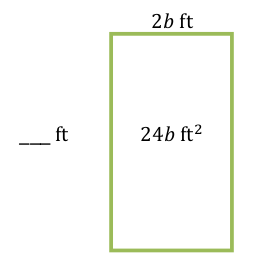
7. The area of the pictured rectangle below is 24b ft 2 . Its width is 2b ft. Find the height of the rectangle and name any properties used with the appropriate step.
[/expand]
[expand title=”Additional Practice”]
Kuta – Simplifying Variable Expressions (With Key)
[/expand]
[expand title=”Assessment”]
Grade 7 PRACTICE Assessment Expressions
Grade 7 Assessment – Expressions
[/expand]
Use variables to represent quantities in a real-world or mathematical problem. (7.EE.4)
[expand title=”Using variables to represent quantities”]
Opening Exercise
Solve the problem using a tape diagram. A sum of money was shared between George and Brian in a ratio of 3: 4. If the sum of money was $56.00, how much did George get?
Exercise 1
Fill in the blanks.
Example 3
Find an equivalent expression by modeling with a rectangular array and applying the distributive property 5(8x + 3).
Exercise 2
For parts (a) and (b), draw a model for each expression and apply the distributive property to expand each expression. Substitute the given numerical values to demonstrate equivalency.
a. 2(x + 1), x = 5
b. 10(2c + 5), c = 1
For parts (c) and (d), apply the distributive property. Substitute the given numerical values to demonstrate equivalency.
c. 3(4f − 1), f = 2
d. 9(−3r − 11), r = 10
Example 4
Rewrite the expression, (6x + 15) ÷ 3, as a sum using the distributive property.
Rewrite ÷ 3 as
Distribute
Multiply
Exercise 3
Rewrite the expressions as a sum.
e. (2b + 12) ÷ 2
f. (20r − 8) ÷ 4
g. (49g − 7) ÷ 7
Example 5
Expand the expression 4(x + y + z).
Exercise 4
Expand the expression from a product to a sum so as to remove grouping symbols using an area model and the repeated use of distributive property: 3(x + 2y + 5z).
Example 6
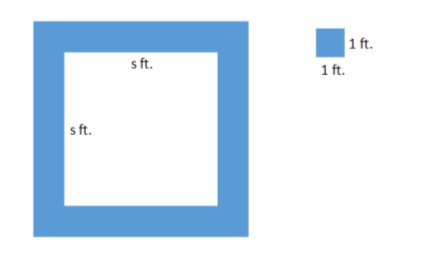
A square fountain area with side length s is bordered by a single row of square tiles as shown. Express the total number of tiles needed in terms of s three different ways.
Problem Set
7.3.1.ProblemSet.UsingVariables
[/expand]
[expand title=”Expressions with Rational Number Coefficients”]
Opening Exercise
Do the computations, leaving your answers in simplest/standard form. Show your steps.
1. Terry weighs 40 kg. Janice weighs kg less than Terry. What is their combined weight?
2.
3.
4.
5. Mr. Jackson bought lbs of beef. He cooked
of it for lunch. How much does he have left?
6.
Exercise 1
For the following exercises, predict how many terms the resulting expression will have after collecting like terms. Then, write the expression in standard form by collecting like terms.
a.
b.
Problem Set
Exercise 3
Rewrite the following expressions in standard form by finding the product and collecting like terms.
a.
b.
c.
Example 4
Model how to write the expression in standard form using rules of rational numbers.
Evaluate the original expression and their answers when x = 20. Do you get the same number?
Exercise 4
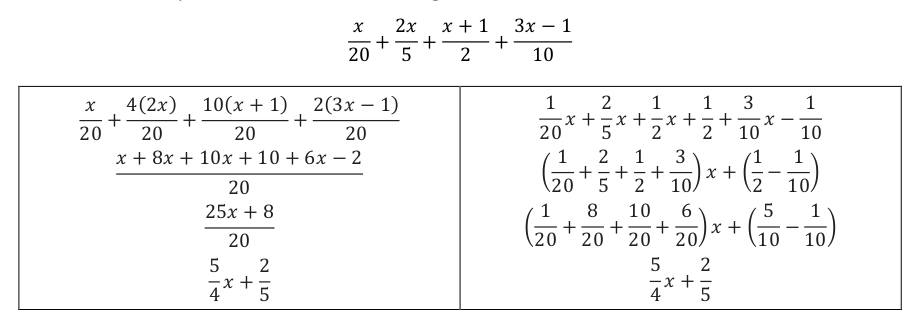
Rewrite the following expression in standard form by finding common denominators and collecting like terms.
Exercise 5
Write the following expression in standard form.
Problem Set
7.3.1.ProblemSet.Rational Coef
[/expand]